Свойства ортогональных проекций
1. Проекция точки есть точка (рис. 1.9).
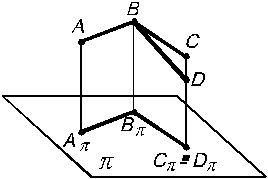
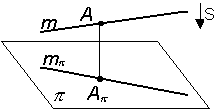
Рис. 1.9 2. Проекция прямой в общем случае есть прямая (рис. 1.10). Если прямая располагается перпендикулярно какой-либо плоскости проекций (такая прямая называется проецирующей), то на эту плоскость она проецируется в виде точки (рис. 1.10). 3. Если точка лежит на прямой, то ее проекция располагается на соответствующей проекции этой же прямой А
Примечание. Первые 3 свойства проекций являются общими для центрального и параллельного проецирования. 4. Если точка делит отрезок прямой в каком-либо отношении, то ее проекция делит проекцию отрезка в том же самом отношении (рис. 1.12).
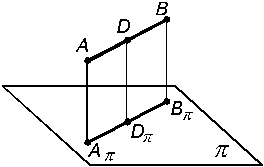
Рис. 1.12 5. Если прямая параллельна плоскости проекций, то на эту плоскость эта прямая проецируется без искажений (рис.1.13). m II Если плоская фигура параллельна плоскости проекций, то на эту плоскость она проецируется без искажения. 6. Если прямые в пространстве пересекаются, то их проекции также пересекаются (рис. 1.14). m
7. Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 1.15). a II b Примечание. Общими для косоугольного и прямоугольного проецирования являются свойства 4, 5, 6. 8. Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется без искажений (рис. 1.16).
Примечание. Свойство 8-е только для ортогонального проецирования. 9. Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.
|

 m
m 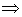 Аp
Аp 

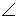
 n = C
n = C 

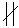 p;
p;