Частные положения прямой в пространстве
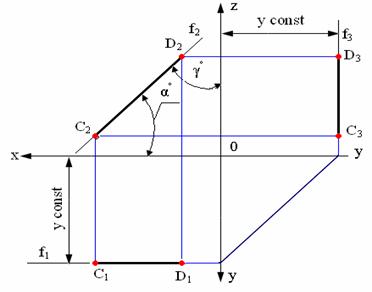
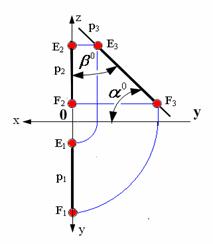
Рис. 2.1. Прямые общего положения На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций. Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций. Рассмотрим изображение на эпюре и отметим основные свойства этих прямых. Прямые, параллельные плоскостям проекций. 1. Горизонтальная прямая h (рис. 2.2) – горизонталь Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π1. Так как все точки этой прямой равноудалены от плоскости проекций π1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π1 проецируются без искажения отрезок прямой АВ (А1В1=АВ) и углы наклона прямой к плоскостям проекций π2 и π3 (углы β0 и γ0). 2. Фронтальная прямая f (рис. 2.3) – фронталь Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π2. Так как все точки этой прямой равноудалены от плоскости проекций π2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π2 проецируются без искажений отрезок этой прямой CD (C2D2+CD) и углы наклона прямой к плоскостям проекций π1 и π3 (углы α 0 и γ 0)
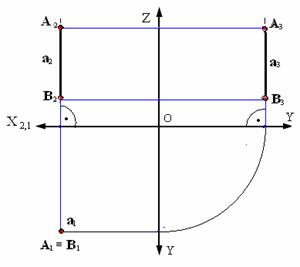
Рис. 2.2. Горизонтальная прямая 3. Профильная прямая p (рис. 2.4) Профильная прямая – это прямая, параллельная профильной плоскости проекций π3 . Так как все точки этой прямой равноудалены от плоскости проекций π3 (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций π3 проецируется без искажения отрезок этой прямой EF (E3F3=EF)и углы наклона прямой к плоскостям проекций π1 и π2 (углы α 0 и β 0). Прямые, принадлежащие плоскостям проекций Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.
Рис. 2.3. Фронтальная прямая
Рис. 2.4. Профильная прямая На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).
Рис. 2.5. Прямая, принадлежащая горизонтальной плоскости проекций
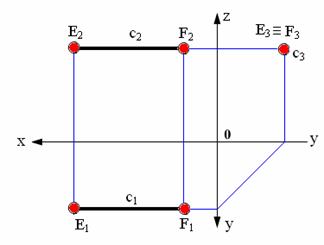
Рис. 2.6. Прямая, принадлежащая фронтальной плоскости проекций
Рис. 2.7. Прямая, принадлежащая профильной плоскости проекций Прямые, перпендикулярные плоскостям проекций. Проецирующие прямые На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π1 в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8). Прямая, перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9). Прямая, перпендикулярная профильной плоскости проекций – профильно-проецирующая прямая. Эта прямая проецируется на плоскость π3 в точку, а ее фронтальная проекция перпендикулярна оси Z. Эти прямые являются частными случаями фронтали и горизонтали.
Рис. 2.8. Прямая, перпендикулярная горизонтальной плоскости проекций
Рис. 2.9. Прямая, перпендикулярная фронтальной плоскости проекций
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций
|

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.


