Проецирование центральное
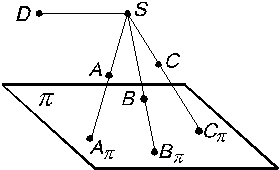
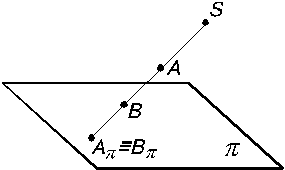
Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. На рис. 1.3 дан пример центрального проецирования, где p – плоскость проекций; S – центр проецирования (точка, не лежащая в плоскости p); А, В, С – точки пространства; Аp, Вp, Сp – центральные проекции точек А, В, С, на плоскость p: они получаются в пересечении проецирующих лучей SA, SB, SC c плоскостью проекций. Если для некоторой точки D проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке. Проекцией точки D будет бесконечно удаленная точка Dp. Проекции точек (А и В), лежащих на одном проецирующем луче, совпадают (Аp
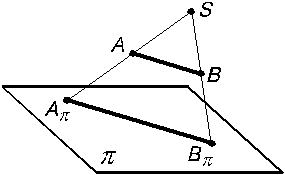
Построение центральных проекций прямой линии АВ и кривой MN показано на (рис. 1.5 и 1.6).
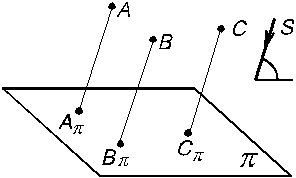
2. Проецирование параллельное Параллельным называется проецирование, при котором все проецирующие лучи между собой параллельны. Параллельные проекции могут быть косоугольными (рис.1.7) и прямоугольными (рис. 1.8).
S – направление проецирования. При косоугольном проецировании проецирующие лучи составляют с плоскостью проекций угол, не равный 90°. При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (прямоугольное проецирование чаще всего называют ортогональным проецированием). Каждый из рассматриваемых способов имеет свои преимущества и недостатки. В зависимости от того, для какой цели выполняется чертеж, используется тот или иной способ. Для выполнения чертежа, по которому изготовляется изображаемый предмет, используется ортогональное проецирование. Косоугольное, параллельное проецирование используется в основном для получения аксонометрических изображений, центральное – для построения перспективных изображений. В изучаемом курсе основное внимание будет уделено ортогональному проецированию.
|

 Вp) (рис. 1.4).
Вp) (рис. 1.4).