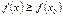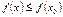Правило №1. Для построения графика функции 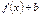 , где
, где  – постоянное число, надо перенести график
– постоянное число, надо перенести график 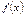 на вектор
на вектор  вдоль оси ординат.
вдоль оси ординат.
Правило №2. Для построения графика функции  , надо растянуть график
, надо растянуть график 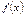 в
в  раз вдоль оси ординат.
раз вдоль оси ординат.
Правило №3. График функции  получается из
получается из
графика 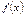 , переносом вдоль оси абсцисс на вектор
, переносом вдоль оси абсцисс на вектор 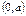
Правило №4. Для построения графика функции  , надо подвергнуть график
, надо подвергнуть график 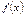 растяжению с коэффициентом
растяжению с коэффициентом  вдоль оси абсцисс.
вдоль оси абсцисс.
Правило №5. Для построения графика функции  , необходимо построить график функции
, необходимо построить график функции 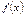 и симметрично его отобразить относительно оси Ox.
и симметрично его отобразить относительно оси Ox.
Правило №6. Если функция периодическая и имеет период 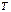 , то функция
, то функция  , где
, где  – постоянны, а
– постоянны, а  , также периодична, причем ее период равен
, также периодична, причем ее период равен 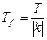
Функция называется четной, если область определения симметрична относительно начала координат и для любого 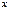 из области определения выполняется равенство
из области определения выполняется равенство 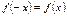 . (График функции симметричен относительно оси ординат).
. (График функции симметричен относительно оси ординат).
Функция называется нечетной, если область определения симметрична относительно начала координат и для любого 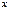 из области определения выполняется равенство
из области определения выполняется равенство 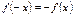 . (График функции симметричен относительно начала координат).
. (График функции симметричен относительно начала координат).
Функция  возрастает на множестве
возрастает на множестве 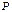 , если для любых
, если для любых 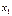 и
и 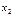 из множества
из множества 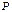 , таких, что
, таких, что 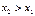 , выполнено неравенство
, выполнено неравенство  .
.
Функция  убывает на множестве
убывает на множестве 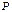 , если для любых
, если для любых 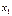 и
и 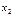 из множества
из множества 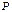 , таких, что
, таких, что 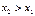 , выполнено неравенство
, выполнено неравенство 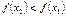 .
.
Точка  называется точкой минимума функции
называется точкой минимума функции  , если для всех
, если для всех 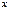 из некоторой окрестности
из некоторой окрестности  выполнено неравенство
выполнено неравенство 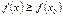
Точка  называется точкой максимума функции
называется точкой максимума функции  , если для всех
, если для всех 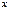 из некоторой окрестности
из некоторой окрестности  выполнено неравенство
выполнено неравенство 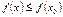

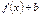 , где
, где  – постоянное число, надо перенести график
– постоянное число, надо перенести график 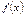 на вектор
на вектор  вдоль оси ординат.
вдоль оси ординат. , надо растянуть график
, надо растянуть график  раз вдоль оси ординат.
раз вдоль оси ординат. получается из
получается из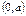
 , надо подвергнуть график
, надо подвергнуть график  , необходимо построить график функции
, необходимо построить график функции 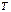 , то функция
, то функция  , где
, где  – постоянны, а
– постоянны, а  , также периодична, причем ее период равен
, также периодична, причем ее период равен 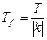
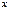 из области определения выполняется равенство
из области определения выполняется равенство 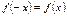 . (График функции симметричен относительно оси ординат).
. (График функции симметричен относительно оси ординат).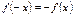 . (График функции симметричен относительно начала координат).
. (График функции симметричен относительно начала координат). возрастает на множестве
возрастает на множестве 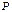 , если для любых
, если для любых 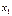 и
и 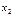 из множества
из множества 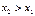 , выполнено неравенство
, выполнено неравенство  .
.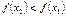 .
. называется точкой минимума функции
называется точкой минимума функции