Выполнение расчета
4.1. Получить решение уравнения теплопроводности для неограниченной пластины при заданных граничных условиях в виде:
где
4.2. По теплофизическим свойствам нержавеющей стали найти значение критерия Био. 4.3. Решить графически характеристическое уравнение, найти корни этого уравнения 4.4. По формуле (10) вычислить коэффициенты 4.5. Для каждого расчетного времени (через 2 минуты) вычислить значения 4.6. Разбить толщину 4.7. Начертить график зависимости 4.8. Найти минимальное время, в течение которого температура поверхности плиты станет равной 4.8.1. Найти время из графика зависимости 4.8.2. Найти время с помощью номограммы 4.9. Вычислить количество теплоты Q, теряемое каждой единицей объёма плиты за время её охлаждения до Вычисление провести тремя способами. 4.9.1. Считать, что к элементу поверхности
В этом случае, допуская, что температура и температурный градиент во всех точках поверхности
4.9.2. Учесть, что элемент объёма
Тогда теплопотери
Обозначив среднюю по всему объёму температуру через
при условии
4.9.3. Считать, что элемент поверхности
где Для нахождения
Здесь принято, что коэффициент теплоотдачи
Вопросы для самостоятельной подготовки 5.1. Получить решение нестационарного уравнения теплопроводности методом разделения переменных. Какой физический смысл имеет коэффициент теплопроводности? В каких единицах измеряется этот коэффициент в СИ? 5.2. Какое граничное условие нужно использовать для получения единственного решения в данной задаче? 5.3. Получите характеристическое уравнение для бесконечной пластины. Как оно решается? 5.4. Каков физический смысл критериев Bi и Fo?
Литература 6.1. Лыков А.В. Теория теплопроводности. – М.; ВШ, 1967. - 599 с. 6.2. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. – М.: Энергоиздат, 1981. – 416 с.
|

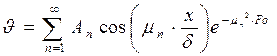 ,
,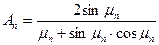 ,
, - корни характеристического уравнения
- корни характеристического уравнения 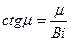 ,
,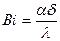 ,
,  - безразмерные критерии Био и Фурье.
- безразмерные критерии Био и Фурье. как точки пересечения кривых
как точки пересечения кривых 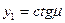 и
и 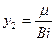 , сравнить их с табличными для данного
, сравнить их с табличными для данного 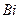 .
.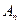 и сравнить их с табличными.
и сравнить их с табличными.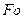 и проверить, как быстро убывают члены ряда (11). Членами ряда, составляющими менее 1% от значения первого члена, пренебречь.
и проверить, как быстро убывают члены ряда (11). Членами ряда, составляющими менее 1% от значения первого члена, пренебречь.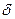 на 15 равных частей и найти безразмерные температуры
на 15 равных частей и найти безразмерные температуры 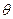 по формуле (11)в этих точках для каждого расчетного момента времени
по формуле (11)в этих точках для каждого расчетного момента времени  .
.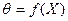 (где
(где 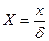 ) - профили температур для этих моментов времени. Кривые распределения температур должны пройти через направляющую точку с безразмерной координатой
) - профили температур для этих моментов времени. Кривые распределения температур должны пройти через направляющую точку с безразмерной координатой 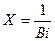 .
.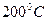 . Воспользоваться для этого двумя способами.
. Воспользоваться для этого двумя способами.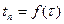 .
.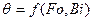 для поверхности пластины.
для поверхности пластины.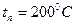 .
.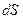 за время
за время 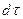 за счет теплопроводности подводится тепло
за счет теплопроводности подводится тепло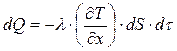 . (12)
. (12) плиты одинаковы, для нахождения
плиты одинаковы, для нахождения  , отданного единицей объёма плиты за время
, отданного единицей объёма плиты за время 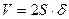 . Тогда получим:
. Тогда получим: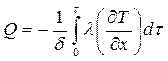 . (13)
. (13)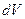 за время
за время 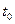 до
до 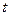 и при этом отдает количество теплоты
и при этом отдает количество теплоты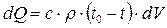 . (14)
. (14)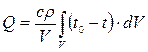 . (15)
. (15)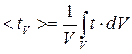 , (16)
, (16)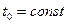 выражение (15) можно записать так:
выражение (15) можно записать так: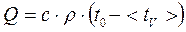 . (17)
. (17) , (18)
, (18)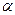 - коэффициент теплоотдачи.
- коэффициент теплоотдачи. . (19)
. (19)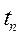 одинаковы для всей поверхности S, причем
одинаковы для всей поверхности S, причем 


