Анализ прохождения гармонического сигнала через нелинейный преобразователь
1) Спектр выходного сигнала при аппроксимации нелинейной ВАХ степенным полиномом Сигнал на выходе нелинейного преобразователя остается периодическим, но перестает быть гармоническим. Можно предположить, что в таком искаженном по форме сигнале появятся дополнительные гармоники. Аппроксимация нелинейной ВАХ:
где
В практических задачах определение коэффициентов Пусть входной сигнал представляет собой гармонику (смещенную):
Подставим в (3):
Заменим степени cos:
Вывод: на выходе нелинейного элемента появляется множество гармоник кратных основной гармонике входного сигнала. Т.о. спектр сигнала на выходе обогащается.
2) Анализ при кусочно-линейной аппроксимации ВАХ.
Аппроксимация:
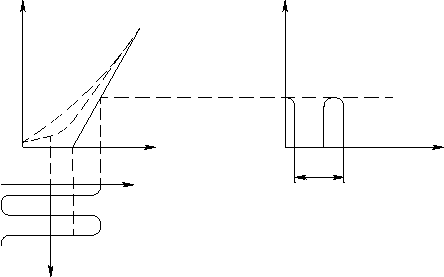
где E 0 – напряжение начала характеристики. Если на входе
Найдем выходной сигнал:
Очевидно, что прерывистый периодический сигнал (6) можно разложить в ряд Фурье и при этом в выходном сигнале появятся новые гармоники, т.е. спектр выходного сигнала обогащается. В чем состоит практическая польза от появления новых высокочастотных гармоник в нелинейных преобразователях? Выгода в том, что высокие частоты на большие расстояния. Более того, информацию низкочастотного характера также легче передать на большие расстояния, если ею промодулировать один из параметров высокочастотного несущего процесса.
|

 , (3)
, (3)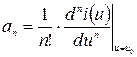 – коэффициент ряда Тейлора;
– коэффициент ряда Тейлора;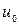 – выбранная точка аппроксимации.
– выбранная точка аппроксимации. в разложении (3) осуществляется решением системы уравнений (сколько неизвестных коэффициентов – столько точек берется на графике), а также методом наименьших квадратов.
в разложении (3) осуществляется решением системы уравнений (сколько неизвестных коэффициентов – столько точек берется на графике), а также методом наименьших квадратов.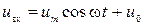
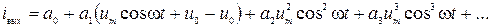

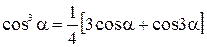
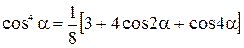
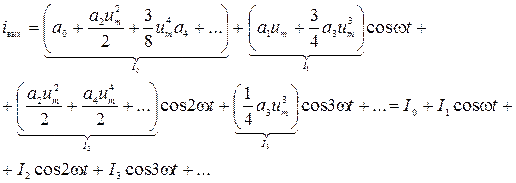 (4)
(4)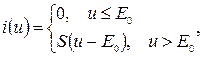
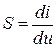 – дифференциальная крутизна характеристики (здесь S = const);
– дифференциальная крутизна характеристики (здесь S = const);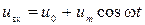 , то на выходе график тока имеет периодический пульсирующий характер и определяется так называемым углом отсечки θ. Найдем связь угла и остальных параметров.
, то на выходе график тока имеет периодический пульсирующий характер и определяется так называемым углом отсечки θ. Найдем связь угла и остальных параметров.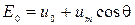 – из графика.
– из графика.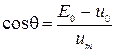 (5) – угол отсечки
(5) – угол отсечки (6)
(6)


