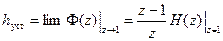Z – преобразования.
Методика расчета: Все приёмы линейной аналоговой техники преобразования применимы к линейным цифровым фильтрам. В частности во временной области отклик аналоговой цепи можно найти как свертку входного воздействия и весовой функции цепи (интеграл Дюамеля), а реакцию цифрового фильтра можно найти в дискретной области как цифровую свертку входной решётчатой функции с решётчатой весовой функцией цифрового фильтра. Интеграл Дюамеля
Второй способ является аналогом операторного метода. Находят z- изображение выходного сигнала, а от него переходят к определению решётчатого выходного процесса, причем двумя вариантами. 1. z- изображение раскладывают на сумму простых дробей, для которых известны по таблицам преобразований оригиналы и решётчатой функции. 2. Дискретные изображения выходного процесса раскладывают в ряд Лорана: Y(z)=X(z)Ф(z)=y0+y1z-1+ y2z-2+… Коэффициенты при z и являются значениями решетчатого выходного процесса. Самый простой вариант разложения это деление многочленов столбиком.
Как оценить качество выходного процесса при задании на входе типового воздействия. Зададим на входе единичную решётчатую функцию (аналог функции Хэвисайда). Реакцией будет решётчатая переходная функция, а графиком является решётчатый переходный процесс и качество будем оценивать по величине перерегулирования и времени дискретного процесса, однако время является целым числом интервалов дискретизации. Изображение выходного сигнала:
вариант а) вариант б) Разложение в ряд Лорана
Коэффициенты разложения в ряд Лорана и дают значение решетчатого выходного процесса Примечание: если входное воздействие – функция Хэвисайда, то выходной процесс является переходным процессом. Имеем:
Трубка точности назначается в виде заранее заданного отклонения в 10% от установившегося значения. Отсюда ясно, что перед построением переходного процесса надо исследовать установившееся значение. При этом существует некоторая аналогия между установлением начального и установившегося значения переходного процесса в операторном преобразовании Лапласа и в дискретном z – преобразовании. В операторном методе:
Или по изображению переходного процесса:
|


 Работа цифрового фильтра происходит таким образом, что его реакцией на первый входной импульс является пачка импульсов весовой функции, каждый из которых умножен на значение входного импульса, реакцией на смещенный второй импульс является такая же смещенная пачка импульсов решётчатой весовой функции цифрового фильтра, умноженной на значение второго импульса и т.д. Полной же реакцией является линейная сумма всех смещенных и масштабируемых копий решётчатой весовой функции цифрового фильтра. Очевидно, что этот способ является громоздким для ручного счета. И этот способ происходит «в слепую», так как трудно судить об окончании этого процесса и приходится делать расчеты с большим запасом.
Работа цифрового фильтра происходит таким образом, что его реакцией на первый входной импульс является пачка импульсов весовой функции, каждый из которых умножен на значение входного импульса, реакцией на смещенный второй импульс является такая же смещенная пачка импульсов решётчатой весовой функции цифрового фильтра, умноженной на значение второго импульса и т.д. Полной же реакцией является линейная сумма всех смещенных и масштабируемых копий решётчатой весовой функции цифрового фильтра. Очевидно, что этот способ является громоздким для ручного счета. И этот способ происходит «в слепую», так как трудно судить об окончании этого процесса и приходится делать расчеты с большим запасом.

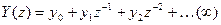 .
. (пока переходный процесс не войдёт в трубку точности).
(пока переходный процесс не войдёт в трубку точности).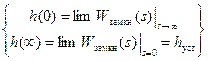 (*)
(*) (**)
(**)