Угловая модуляция сигналов
Несущее колебание:
Если частоту менять по закону Пусть Тогда несущее колебание превратится в:
Изменения фазы – девиация фазы:
Соотношение:
Следовательно:
Если менять частоту по закону:
то получим ЧМ-сигнал:
(15) – аналитическая запись ЧМ-сигнала. При плавном изменении модулирующего воздействия по форме ФМ и ЧМ сигнала совпадут, но между ними есть принципиальная разница, а именно – сдвиг фазы между ФМ-сигналом и несущим колебанием пропорционален модулирующему воздействию
Анализ сигналов с угловой модуляцией является гораздо более сложным, чем сигналов с АМ. Рассмотрим в связи с этим случай однотональной угловой модуляции. Пусть частота меняется по закону:
где
Полная фаза
Если менять частоту:
взяли
Эта m играет такую же роль, как и в АМ. Таким образом, сигнал с ЧМ может быть записан в виде:
Исследование спектра сигнала с угловой модуляцией даже при однотональной модуляции гораздо сложнее, чем АМ-сигнала. При любом значении m исследование спектра проводят с помощью так называемой функции Бесселя. А при неглубокой модуляции ( Пусть
Разложим в ряд Тейлора:
Из разложения (
(22) соответствует спектру однотональной АМ. Тем не менее, есть разница, состоящая в том, что фаза нижней боковой составляющей отличается от таковой при АМ-модуляции на 180º. Более точный анализ получим, если учтем по 2 члена разложения ( Таким образом, даже при однотональной модуляции спектр ЧМ и ФМ-сигналов намного сложнее, чем АМ и имеют боковые полосы, и естественно имеют соответствующие перераспределение энергии между несущей частотой и боковыми частотами.
|

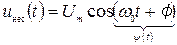
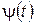 – полная фаза (фазовый угол)
– полная фаза (фазовый угол)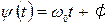
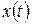 , то имеем частотную модуляцию (ЧМ), если фаза – фазовую модуляцию (ФМ). Обе вместе – угловая модуляция (УМ).
, то имеем частотную модуляцию (ЧМ), если фаза – фазовую модуляцию (ФМ). Обе вместе – угловая модуляция (УМ). (10)
(10)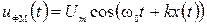 (11) – ФМ-сигнал
(11) – ФМ-сигнал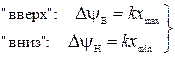 (12)
(12)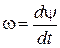
 (13)
(13)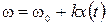 , (14)
, (14) (15)
(15) (16)
(16)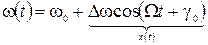 , (17)
, (17)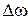 – девиация частоты;
– девиация частоты;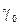 – начальные фазы.
– начальные фазы.
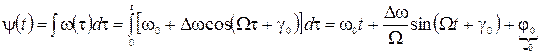
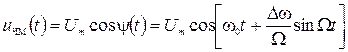 (18)
(18)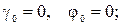
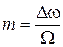 – индекс однотональной угловой модуляции (19)
– индекс однотональной угловой модуляции (19)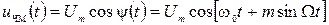 (20)
(20)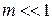 ) удается разложить гармоники в ряд и исследовать спектр ЧМ и ФМ-сигналов.
) удается разложить гармоники в ряд и исследовать спектр ЧМ и ФМ-сигналов.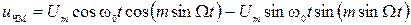 (21)
(21)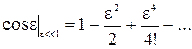
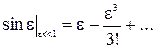

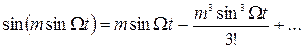 (
( )
) (22)
(22)


