1. На одной стороне угла с вершиной S отмечены точки D и B, причем SB > SD, на другой стороне – точки C и E. SD = SC, SB = SE. Докажите, что КB = КE, где К = DE 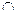 CB.
CB.
 Дано:
Дано:  S, SB>SD. SB=SE, SD=SC.
S, SB>SD. SB=SE, SD=SC.
Доказать: KB=KE.
Док-во: 1)Рассмотрим треугольники BSC и ESD.  BSC =
BSC =  ESD по двум сторонам и углу между ними, т.к. SC=SD – по условию, SB=SE – по условию,
ESD по двум сторонам и углу между ними, т.к. SC=SD – по условию, SB=SE – по условию,  S - общий.
S - общий.
2) Рассмотрим треугольники KDB и KCE.
a) Видим, что DB=CE как разности равных отрезков, т.е. DB=SB-SD, CE=SE-SC. b)  BDK=
BDK=  ECK как смежные с равными углами, т.е.
ECK как смежные с равными углами, т.е.  BDK=1800-
BDK=1800-  SDE
SDE  ECK=1800-
ECK=1800-  SCB.
SCB.
c)  DBK=
DBK=  CEX, т.к.
CEX, т.к.  BSC =
BSC =  ESD. Т.о.
ESD. Т.о.  KDB =
KDB =  KCE, а значит, KB=KE.
KCE, а значит, KB=KE.
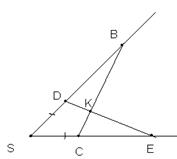
2. В треугольнике АВС проведена медиана АА1. На ней задана точка К такая, что  СКА1 =
СКА1 =  А1КВ. Докажите, что треугольник АВС – равнобедренный.
А1КВ. Докажите, что треугольник АВС – равнобедренный.
 Дано:
Дано:  АВС, АА1 – медиана,
АВС, АА1 – медиана,  СКА1 =
СКА1 =  А1КВ.
А1КВ.
Доказать:  АВС - равнобедренный.
АВС - равнобедренный.
Док-во: 1)Рассмотрим  CКВ. Отрезок КА1 является медианой и биссектрисой, значит,
CКВ. Отрезок КА1 является медианой и биссектрисой, значит,  CКВ равнобедренный, и СК = КВ.
CКВ равнобедренный, и СК = КВ.
2)  АСК =
АСК =  АВК (по двум сторонам и углу между ними). Т.к. АК – общая, СК=КВ по доказанному,
АВК (по двум сторонам и углу между ними). Т.к. АК – общая, СК=КВ по доказанному,  АКС=
АКС=  АКВ, как смежные с равными углами СКА1 и А1КВ.
АКВ, как смежные с равными углами СКА1 и А1КВ.
3) Из равенства треугольников АСК и АВК, следует, что АС=АВ, т.е. треугольник АВС - равнобедренный.
3. Докажите, что вершины В и С треугольника АВС равноудалены от медианы ma.
 Дано:
Дано:  АВС, АМ- медиана, М
АВС, АМ- медиана, М  ВС, ВМ=МС, ВВ1
ВС, ВМ=МС, ВВ1  АМ, В1
АМ, В1  АМ, СС1
АМ, СС1  АМ, С1
АМ, С1  АМ. Доказать: ВВ1=СС1.
АМ. Доказать: ВВ1=СС1.
Док-во: 1)  СС1М =
СС1М =  ВВ1М (по гипотенузе и острому углу). Т.к. СМ=МВ,
ВВ1М (по гипотенузе и острому углу). Т.к. СМ=МВ,  СМС1=
СМС1=  ВМВ1, как вертикальные.
ВМВ1, как вертикальные.
2) Из равенства треугольников СС1М и ВВ1М, следует равенство их катетов СС1 и ВВ1.
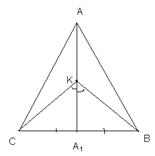
4. В треугольнике АВС проведена биссектриса ВВ1. Пусть М – такая точка плоскости, что отрезок МВ1 пересекает сторону ВС в точке К. ВМ = АВ1,  МВВ1 =
МВВ1 =  ВВ1А. Докажите, что ВК = КВ1.
ВВ1А. Докажите, что ВК = КВ1.
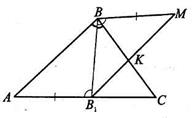 Дано:
Дано:  АВС, ВВ1- биссектриса,
АВС, ВВ1- биссектриса,  АВВ1=
АВВ1=  В1ВС. К
В1ВС. К  ВС, ВМ=АВ1.
ВС, ВМ=АВ1.  МВВ1=
МВВ1=  ВВ1А. Доказать: ВК = КВ1.
ВВ1А. Доказать: ВК = КВ1.
Доказательство:
1)  АВ1В =
АВ1В =  МВВ1 (по двум сторонам и углу между ними). Т.к. ВМ=АВ1, ВВ1 – общая,
МВВ1 (по двум сторонам и углу между ними). Т.к. ВМ=АВ1, ВВ1 – общая,  ВВ1А=
ВВ1А=  МВВ1.
МВВ1.
2) Тогда  АВВ1=
АВВ1=  ВВ1М как углы, лежащие против равных сторон АВ1 и ВМ в равных треугольниках АВ1В и МВВ1.
ВВ1М как углы, лежащие против равных сторон АВ1 и ВМ в равных треугольниках АВ1В и МВВ1.
3) Получили, что  АВВ1=
АВВ1=  ВВ1М, и
ВВ1М, и  АВВ1=
АВВ1=  В1ВС (т.к. ВВ1- биссектриса угла АВС). Значит,
В1ВС (т.к. ВВ1- биссектриса угла АВС). Значит,  ВВ1М=
ВВ1М=  ВВ1К, т.е.
ВВ1К, т.е.  ВВ1К – равнобедренный. Следовательно, ВК = КВ1.
ВВ1К – равнобедренный. Следовательно, ВК = КВ1.
5. Докажите, что если угол и две высоты одного треугольника соответственно равны углу и двум высотам второго треугольника, то эти треугольники равны.
 Решение: Выделим в этой задаче два случая: а) когда в каждом треугольнике обе данные высоты проведены к сторонам равных углов; б) когда одна из высот каждого треугольника проведена к стороне, противолежащей данному углу.
Решение: Выделим в этой задаче два случая: а) когда в каждом треугольнике обе данные высоты проведены к сторонам равных углов; б) когда одна из высот каждого треугольника проведена к стороне, противолежащей данному углу.
Случай а)
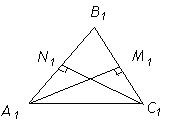 Дано:
Дано:  АВС,
АВС,  А1В1С1.
А1В1С1.  B =
B =  B1, AM
B1, AM  BC, M
BC, M  BC, CN
BC, CN  AB, N
AB, N  AB, A1M1
AB, A1M1  BlC1, M1
BlC1, M1  BlCl, ClNl
BlCl, ClNl  AlBl, AM=AlMl, CN = ClNl. Доказать:
AlBl, AM=AlMl, CN = ClNl. Доказать:  АВС=
АВС=  А1В1С1.
А1В1С1.
Док-во: 1)  АMВ =
АMВ =  A1M1В1 (по катету и острому углу). Т.к. AM=AlMl,
A1M1В1 (по катету и острому углу). Т.к. AM=AlMl,  B =
B =  B1. Следовательно, АВ=А1В1.
B1. Следовательно, АВ=А1В1.
2)  CNВ =
CNВ =  C1N1В1 (по катету и острому углу). Т.к. CN = ClNl,
C1N1В1 (по катету и острому углу). Т.к. CN = ClNl,  B =
B =  B1. Следовательно, ВС=В1С1.
B1. Следовательно, ВС=В1С1.
 3)
3)  АВС =
АВС =  А1В1Cl (по двум сторонам и углу между ними). Т.к. АВ=А1В1, ВС=В1С1,
А1В1Cl (по двум сторонам и углу между ними). Т.к. АВ=А1В1, ВС=В1С1,  B =
B =  B1.
B1.
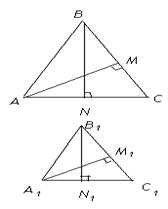
Случай б)
Дано:  АВС,
АВС,  А1В1С1.
А1В1С1.  B =
B =  B1, AM
B1, AM  BC, M
BC, M  BC, BN
BC, BN  AC, N
AC, N  AB, A1M1
AB, A1M1  BlC1, M1
BlC1, M1  BlCl, BlNl
BlCl, BlNl  AlCl, AM=AlMl, BN = BlNl.
AlCl, AM=AlMl, BN = BlNl.
Доказать:  АВС=
АВС=  А1В1С1.
А1В1С1.
Доказательство: 1)  АMВ=
АMВ=  A1M1В1 (по катету и острому углу). Т.к. AM=AlMl,
A1M1В1 (по катету и острому углу). Т.к. AM=AlMl,  B =
B =  B1. Следовательно, АВ=А1В1.
B1. Следовательно, АВ=А1В1.
2)  ANВ=
ANВ=  A1N1В1 (по катету и гипотенузе). Т.к. BN = BlNl, АВ=А1В1. Следовательно,
A1N1В1 (по катету и гипотенузе). Т.к. BN = BlNl, АВ=А1В1. Следовательно,  A =
A =  A1.
A1.
3)  АВС =
АВС =  А1В1Cl (по стороне и прилежащим к ней углам).
А1В1Cl (по стороне и прилежащим к ней углам).
Т.к. АВ=А1В1,  A =
A =  A1,
A1,  B =
B =  B1.
B1.
6. Угол ВАС равен 300. Из точки D стороны АВ опущен перпендикуляр DE на сторону АС; из точки Е опущен перпендикуляр EF на сторону АВ; из точки F – перпендикуляр FM на сторону АС. Вычислите FM, если DE равен 10.

| Дано:  АВС=300, D АВС=300, D  AB, DE AB, DE  AC, E=DE AC, E=DE  AC, EF AC, EF  AB, F=EF AB, F=EF  AB, FM AB, FM  AC, M=FM AC, M=FM 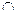 AC, DE=10. Найти: FM.
Решение:
1) Рассмотрим AC, DE=10. Найти: FM.
Решение:
1) Рассмотрим  АDE. Он прямоугольный (DE АDE. Он прямоугольный (DE  AЕ), AЕ),  DAE=300, значит, AD=2DE=20.
2) DAE=300, значит, AD=2DE=20.
2)  DAE = DAE =  DEF, как острые углы со взаимно перпендикулярными сторонами (DE DEF, как острые углы со взаимно перпендикулярными сторонами (DE  AC, EF AC, EF  AD).
3) Тогда в AD).
3) Тогда в  FED FED  DFE=900, DFE=900,  FED=300, то FD= FED=300, то FD= 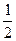 DE=5.
4) AF=AD-FD=20-5=15.
5) В DE=5.
4) AF=AD-FD=20-5=15.
5) В  AMF AMF  AMF=900, AMF=900,  FAM=300, то FM= FAM=300, то FM= 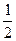 AF=7,5. AF=7,5.
|
7. Докажите, что если высота треугольника делит его периметр пополам, то треугольник равнобедренный.
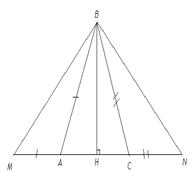
| Дано:  АВС=300, BH АВС=300, BH  AC, AB+AH=HC+BC. Доказать: АВ=ВС.
Доказательство:
1) На продолжении стороны АС за точку А отложим отрезок АМ, равный АВ. На продолжении СА за точку С отложим отрезок СN, равный ВС.
2) Получим МА+АН=НС+СN, так как по условию АВ+АН=НС+ВС, ВН AC, AB+AH=HC+BC. Доказать: АВ=ВС.
Доказательство:
1) На продолжении стороны АС за точку А отложим отрезок АМ, равный АВ. На продолжении СА за точку С отложим отрезок СN, равный ВС.
2) Получим МА+АН=НС+СN, так как по условию АВ+АН=НС+ВС, ВН  MN. Следовательно, треугольник MBN-равнобедренный, т.е. MN. Следовательно, треугольник MBN-равнобедренный, т.е.  M= M=  N. (*)
3) N. (*)
3)  BAH = BAH =  BMA+ BMA+  ABM, т.е. ABM, т.е.  BAH =2 BAH =2  M (1), т.к. AM=AB, а значит, M (1), т.к. AM=AB, а значит,  AMB= AMB=  ABM.
4) ABM.
4)  BCH=2 BCH=2  N (2).
5) Из (1), (2) и (*) следует, что N (2).
5) Из (1), (2) и (*) следует, что  ВАН= ВАН=  ВСН, т.е. треугольник АВС равнобедренный. ВСН, т.е. треугольник АВС равнобедренный.
|
8. Докажите, что если биссектриса треугольника делит его периметр пополам, то треугольник равнобедренный.
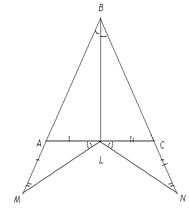
| Дано:  АВС, АВС,  ABL= ABL=  LBC, L=BL LBC, L=BL 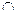 AC, AB+AL=LC+BC.
Доказать: АВ=ВС.
Доказательство:
1) На продолжении стороны BA за точку А отложим отрезок АМ, равный АL.
2) На продолжении BС за точку С отложим отрезок СN, равный LС.
3) Тогда получим BА+АM=BС+СN, так как по условию АВ+АL=BС+CL.
4) AC, AB+AL=LC+BC.
Доказать: АВ=ВС.
Доказательство:
1) На продолжении стороны BA за точку А отложим отрезок АМ, равный АL.
2) На продолжении BС за точку С отложим отрезок СN, равный LС.
3) Тогда получим BА+АM=BС+СN, так как по условию АВ+АL=BС+CL.
4)  BML = BML =  BNL по двум сторонам и углу между ними. Т.к. BL- общая, BM=BN, и BNL по двум сторонам и углу между ними. Т.к. BL- общая, BM=BN, и  MBL= MBL=  LBN.
5) Из равенства треугольников BML и BNL следует равенство углов M и N и сторон ML и LN.
6) LBN.
5) Из равенства треугольников BML и BNL следует равенство углов M и N и сторон ML и LN.
6)  AML = AML =  CNL по стороне и двум прилежащим углам. Т.к. ML=LN, CNL по стороне и двум прилежащим углам. Т.к. ML=LN,  AML= AML=  ALM, ALM,  CLN = CLN =  CNL, CNL,  AML = AML =  CNL.
7) Значит, AL=LC, и BL – биссектриса, т.е. треугольник АВС равнобедренный. CNL.
7) Значит, AL=LC, и BL – биссектриса, т.е. треугольник АВС равнобедренный.
|
9. Найти углы треугольника, в котором высота и медиана, проведенные из одной вершины, делят угол при этой вершине на три равные части.
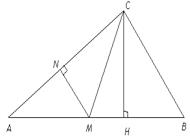
| Дано:  АВС, М АВС, М  AB, АМ=МВ, СН AB, АМ=МВ, СН  AВ, Н AВ, Н  AB, AB,  AСМ= AСМ=  МCН= МCН=  НСВ. Найти: НСВ. Найти:  А, А,  В, В,  С.
Решение:
1)Пусть НВ=х, тогда МН=х, т.к. С.
Решение:
1)Пусть НВ=х, тогда МН=х, т.к.  МСН= МСН=  BСН ( BСН ( МНС = МНС =  СНВ = 900, СН-общая, СНВ = 900, СН-общая,  МСН= МСН=  НСВ). Значит, АМ=2х, т.к. АМ=МВ.
2) Проведем MN НСВ). Значит, АМ=2х, т.к. АМ=МВ.
2) Проведем MN  AС, N=MN AС, N=MN 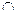 AC. Тогда AC. Тогда  СMN = СMN =  CMH, т.к. CMH, т.к.  СNM= СNM=  CHM=900, CM- общая сторона, CHM=900, CM- общая сторона,  NСM= NСM=  HСM. Значит,MN=x.
3) HСM. Значит,MN=x.
3)  ANM – прямоугольный, ANM – прямоугольный,  ANM=900, MN=x, AM=2x. Тогда катет MN лежит против угла NAM и равен половине гипотенузы АМ. Значит, ANM=900, MN=x, AM=2x. Тогда катет MN лежит против угла NAM и равен половине гипотенузы АМ. Значит,  CHM=300.
4) Из прямоугольного CHM=300.
4) Из прямоугольного  АСН получаем, что АСН получаем, что  АСН=600, значит, АСН=600, значит,  AСВ=900, AСВ=900,  СВА=600. Ответ: 300, 900, 600. СВА=600. Ответ: 300, 900, 600.
|

 CB.
CB. Дано:
Дано:  S, SB>SD. SB=SE, SD=SC.
S, SB>SD. SB=SE, SD=SC. BSC =
BSC =  Дано:
Дано:  Дано:
Дано:  ВС, ВМ=МС, ВВ1
ВС, ВМ=МС, ВВ1  АМ, В1
АМ, В1  Дано:
Дано:  Решение: Выделим в этой задаче два случая: а) когда в каждом треугольнике обе данные высоты проведены к сторонам равных углов; б) когда одна из высот каждого треугольника проведена к стороне, противолежащей данному углу.
Решение: Выделим в этой задаче два случая: а) когда в каждом треугольнике обе данные высоты проведены к сторонам равных углов; б) когда одна из высот каждого треугольника проведена к стороне, противолежащей данному углу. Дано:
Дано:  3)
3) 
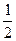 DE=5.
4) AF=AD-FD=20-5=15.
5) В
DE=5.
4) AF=AD-FD=20-5=15.
5) В 





