10. Доказать, что если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого, то такие треугольники подобны.

| Дано:  АВС, АВС,  А1В1С1. А1В1С1.  С = С =  С1=900, С1=900,  .
Доказать: .
Доказать:  АВС ~ АВС ~  А1В1С1.
Доказательство:
1) На луче АС от т. С отложим отрезок СМ, равный ClA1.
2) Проведем прямую через точку М, параллельно АВ. Пусть А1В1С1.
Доказательство:
1) На луче АС от т. С отложим отрезок СМ, равный ClA1.
2) Проведем прямую через точку М, параллельно АВ. Пусть 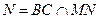 . Получим . Получим  MNC.
3) MNC.
3)  MNC ~ MNC ~  АВС (по двум углам).
Т.к. АВС (по двум углам).
Т.к.  AВС = AВС =  MNC – по построению, MNC – по построению,  С - общий. Из подобия треугольников следует: С - общий. Из подобия треугольников следует: 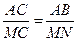 .
4) Из условия задачи имеем .
4) Из условия задачи имеем  . Тогда . Тогда
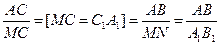 . Или по другому . Или по другому  . Отсюда А1В1=MN. Следовательно, . Отсюда А1В1=MN. Следовательно,  MNC = MNC =  А1В1Cl (по гипотенузе и катету).
Т.к. MN=А1В1, MC= ClA1. А значит, получили доказываемое, т.е. А1В1Cl (по гипотенузе и катету).
Т.к. MN=А1В1, MC= ClA1. А значит, получили доказываемое, т.е.  АВС ~ АВС ~  А1В1С1. А1В1С1.
|
11. Стороны треугольника относятся как 4: 5: 6. Найдите стороны треугольника, подобного данному, если меньшая сторона второго треугольника равна 0,8 см.
Решение: Итак, нужно найти две оставшиеся стороны второго треугольника. Т.к. треугольники подобны, то для второго треугольника верна пропорция, тогда, пусть х- коэффициент подобия, Но тогда стороны второго треугольника равны 4х, 5х и 6х. Отсюда получаем, 4х=0.8 или х=0.2. Тогда стороны равны: 0.8, 1, 1.2. Ответ: 0.8, 1, 1.2.
12. Докажите, что в подобных треугольниках сходственные стороны пропорциональны сходственным высотам, т.е. тем высотам, которые опущены на сходственные стороны.

| Дано:  АВС, ~ АВС, ~  А1В1С1. А1В1С1. 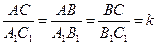 , BH , BH  AC, B1H1 AC, B1H1  A1C1.
Доказать: A1C1.
Доказать: 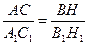 .
Доказательство:
1) .
Доказательство:
1)  ABH ~ ABH ~  A1B1H1 (по двум углам).
Т.к. A1B1H1 (по двум углам).
Т.к.  A = A =  A1 (из подобия треугольников АВС и А1В1С1), A1 (из подобия треугольников АВС и А1В1С1),  AHB = AHB =  A1H1B1= 900. Из подобия треугольников следует: A1H1B1= 900. Из подобия треугольников следует:  . Но . Но 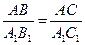 . Тогда . Тогда 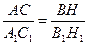 .
Аналогично можно доказывать, что сходственные стороны пропорциональны сходственным биссектрисам, медианам. .
Аналогично можно доказывать, что сходственные стороны пропорциональны сходственным биссектрисам, медианам.
|
13. В остроугольном треугольнике АВС проведены неравные высоты АМ и ВN. 1)Докажите, что треугольники АМС и ВNС подобны. 2) Докажите, что треугольник MNC подобен треугольнику АВС. Вычислите коэффициент подобия этих треугольников.
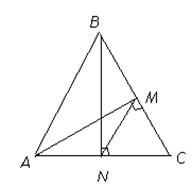
| Дано:  АВС. AM АВС. AM  BC, BN BC, BN  AC.
Доказать: 1) AC.
Доказать: 1)  AMC ~ AMC ~  BNC. 2) BNC. 2)  MNC ~ MNC ~  ABC. 3) k-?
Доказательство:
1) ABC. 3) k-?
Доказательство:
1)  AMC ~ AMC ~  BNC (по двум углам).
Т.к. BNC (по двум углам).
Т.к.  BNC = BNC =  AMC = 900, AMC = 900,  C- общий. Из подобия треугольников следует: C- общий. Из подобия треугольников следует:  .
2) .
2)  MNC ~ MNC ~  ABC (по двум сторонам и углу между ними).
Т.к. ABC (по двум сторонам и углу между ними).
Т.к.  . Т.е. получили, что стороны образующие угол С, пропорциональны. И . Т.е. получили, что стороны образующие угол С, пропорциональны. И  C- общий.
3) Найдем коэффициент подобия C- общий.
3) Найдем коэффициент подобия  ABC и ABC и  MNC. Для этого рассмотрим MNC. Для этого рассмотрим  АMC. АMC.  . И т.к. из подобия треугольников . И т.к. из подобия треугольников  ABC и ABC и  MNC верна пропорция AC∙NC=BC∙MC. Т.е. MNC верна пропорция AC∙NC=BC∙MC. Т.е. 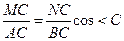 . k = cos<C. . k = cos<C.
|
14. Доказать, что биссектриса внешнего угла треугольника пересекает продолжение противоположной стороны в точке, расстояния от которой до концов этой стороны пропорциональны прилежащим сторонам треугольника.
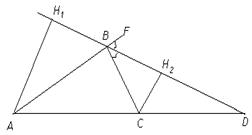
| Дано:  АВС. <FBC – внешний угол. BD – биссектриса.
Доказать: АВС. <FBC – внешний угол. BD – биссектриса.
Доказать:  .
Доказательство:
1) Проведем перпендикуляры СH2 и AH1.
2) .
Доказательство:
1) Проведем перпендикуляры СH2 и AH1.
2)  AH1B ~ AH1B ~  CH2B (по двум углам).
Т.к. CH2B (по двум углам).
Т.к.  AH1B = AH1B =  CH2B = 900, CH2B = 900,  H1BA = H1BA =  FBH2= FBH2=  H2BC (вертикальные). Из подобия треугольников следует: H2BC (вертикальные). Из подобия треугольников следует:  . (1)
3) СH2 || AH1.
4) . (1)
3) СH2 || AH1.
4)  AH1D ~ AH1D ~  CH2D (по двум углам).
Т.к. CH2D (по двум углам).
Т.к.  D- общий, <AH1D = D- общий, <AH1D =  CH2D= 900. Из подобия треугольников следует: CH2D= 900. Из подобия треугольников следует: 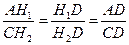 . (2).
5) Из равенств (1) и (2) следует . (2).
5) Из равенств (1) и (2) следует  . .
|
15. На высотах ВВ1 и СС1 треугольника АВС взяты точки В2 и С2 так, что <AB2C = <AC2B = 900. Докажите, что АВ2 = АС2.

| Дано:  АВС. BB1 АВС. BB1  AC, CC1 AC, CC1  AB <AB2C=<AC2B = 900.
Доказать: AB2=AC2.
Доказательство:
1) Соединим С1 и В1, получим треугольник АС1В1.
2) AB <AB2C=<AC2B = 900.
Доказать: AB2=AC2.
Доказательство:
1) Соединим С1 и В1, получим треугольник АС1В1.
2)  AС1B1 ~ AС1B1 ~  АBС (по двум сторонам и углу между ними).
Т.к. АBС (по двум сторонам и углу между ними).
Т.к.  A – общий, а образующие его стороны пропорциональны, см задачу № 14. Из подобия треугольников следует: A – общий, а образующие его стороны пропорциональны, см задачу № 14. Из подобия треугольников следует:  . (1)
3) В . (1)
3) В  АВ2С – угол АВ2С= 900. В2В1 – высота из прямого угла на гипотенузу АС.
Отсюда АВ2С – угол АВ2С= 900. В2В1 – высота из прямого угла на гипотенузу АС.
Отсюда 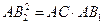 . (2)
4) В . (2)
4) В  АС2В – угол АС2В= 900. С2С1 – высота из прямого угла на гипотенузу АВ.
Отсюда АС2В – угол АС2В= 900. С2С1 – высота из прямого угла на гипотенузу АВ.
Отсюда 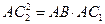 . (3)
5) Из равенств (1), (2) и (3) следует: . (3)
5) Из равенств (1), (2) и (3) следует:
 . Т.е. . Т.е.
 . Отсюда . Отсюда  . .
|
16. В подобных треугольниках из вершин равных углов проведены высота и биссектриса. 1) Докажите, что углы между высотой и биссектрисой в обоих треугольниках равны. 2) Докажите, что будут равны углы между любыми сходственными высотами и биссектрисами подобных треугольников (т.е. высоты проведены к сходственным сторонам, а биссектрисы – из вершин равных углов).
а) 1 случай:

| Дано:  АВС~ АВС~  А1В1С1. <B=<B1, BH А1В1С1. <B=<B1, BH  AC, B1H1 AC, B1H1  A1C1, BL, B1L1 – биссектрисы, <ABL = <LBC, <A1B1L1 = <L1B1C1.
Доказать: <LBH=<L1B1H1.
Доказательство:
1) A1C1, BL, B1L1 – биссектрисы, <ABL = <LBC, <A1B1L1 = <L1B1C1.
Доказать: <LBH=<L1B1H1.
Доказательство:
1)  ABL ~ ABL ~  A1B1L1 (по двум углам).
Т.к. A1B1L1 (по двум углам).
Т.к.  A = A =  A1, (из подобия треугольников A1, (из подобия треугольников  АВС~ АВС~  А1В1С1), А1В1С1),  ABL = ABL =  A1B1L1 (по условию).
Из подобия треугольников следует: A1B1L1 (по условию).
Из подобия треугольников следует:  . (1)
2) . (1)
2)  ABH ~ ABH ~  A1B1H1 (по двум углам).
Т.к. A1B1H1 (по двум углам).
Т.к.  A = A =  A1, (из подобия треугольников A1, (из подобия треугольников  АВС~ АВС~  А1В1С1), А1В1С1),  AHB = AHB =  A1H1B1 == 900.
Из подобия треугольников следует: A1H1B1 == 900.
Из подобия треугольников следует:
 . (2)
3) Из (1) и (2) следует . (2)
3) Из (1) и (2) следует   .
Отсюда .
Отсюда  LHB ~ LHB ~  L1H1B1. Тогда <LBH = <L1B1H1. L1H1B1. Тогда <LBH = <L1B1H1.
|
б) 2 случай:
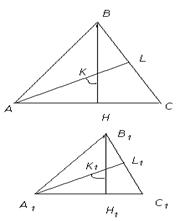
| Дано:  АВС~ АВС~  А1В1С1. <A=<A1, BH А1В1С1. <A=<A1, BH  AC, B1H1 AC, B1H1  A1C1, AL, A1L1 – биссектрисы, <BAL = <LAC= <B1A1L1 = <L1A1C1.
Доказать: <AKH=<A1K1H1.
Доказательство:
1) A1C1, AL, A1L1 – биссектрисы, <BAL = <LAC= <B1A1L1 = <L1A1C1.
Доказать: <AKH=<A1K1H1.
Доказательство:
1)  AKH ~ AKH ~  A1K1H1 (по двум углам).
Т.к. A1K1H1 (по двум углам).
Т.к.  AHK = AHK =  A1H1K1= 900, <LAC=<L1A1C1.
Тогда <AKH=<A1K1H1. A1H1K1= 900, <LAC=<L1A1C1.
Тогда <AKH=<A1K1H1.
|
17. В треугольнике АВС известно, что ВС = 12 см, АС = 8 см и угол А вдвое больше угла В. Найдите АВ.

| Дано:  АВС. <A=2<B, BC=12, AC=8. Найти: АВ.
Решение: 1) Проведем биссектрису угла А. Получили АВС. <A=2<B, BC=12, AC=8. Найти: АВ.
Решение: 1) Проведем биссектрису угла А. Получили  АКВ – равнобедренный, АК=КВ.
2) АКВ – равнобедренный, АК=КВ.
2)  AKС ~ AKС ~  AВС (по двум углам).
Т.к. AВС (по двум углам).
Т.к.  С – общий, С – общий,  САК= <В. Из подобия треугольников следует: САК= <В. Из подобия треугольников следует: 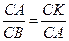 . Отсюда СК= . Отсюда СК=  . СК=КВ=12- . СК=КВ=12- 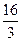 = =  . . 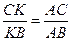 . Отсюда АВ= . Отсюда АВ= 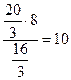 . Ответ: 10. . Ответ: 10.
|
18. Доказать, что две параллельные прямые, пересекаемые рядом прямых, исходящих из одной и той же точки, рассекаются ими на пропорциональные части.

| Дано: a||b, c 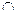 d d 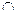 e=O. Доказать: e=O. Доказать:  .
Доказательство:
1) .
Доказательство:
1)  AOB ~ AOB ~  A1OB1 (по двум сторонам и углу между ними).
Т.к. A1OB1 (по двум сторонам и углу между ними).
Т.к.  О – общий, О – общий, 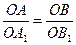 , по теореме о пропорциональных отрезках. Из подобия следует: , по теореме о пропорциональных отрезках. Из подобия следует:  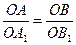 .
2) .
2)  OBС ~ OBС ~  OB1С1 (по двум сторонам и углу между ними).
Т.к. OB1С1 (по двум сторонам и углу между ними).
Т.к.  О – общий, О – общий, 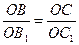 , по теореме о пропорциональных отрезках. Из подобия следует: , по теореме о пропорциональных отрезках. Из подобия следует: 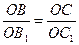  .
Тогда .
Тогда  . .
|
19. На стороне ВС треугольника АВС взята точка А1 так, что  . В каком отношении медиана СС1 делит отрезок АА1?
. В каком отношении медиана СС1 делит отрезок АА1?
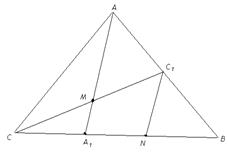
| Дано:  АВС. А1 АВС. А1  СВ, ВА1:А1С = 2:1, С1 СВ, ВА1:А1С = 2:1, С1  АВ. АС1=С1В. М=АА1 АВ. АС1=С1В. М=АА1 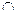 СС1. Найти: AМ: МА1.
Решение: 1) Выберем на отрезке А1В т. N, так что A1N=NB=CA1. Соединим N с C1.
2) NC1 – средняя линия СС1. Найти: AМ: МА1.
Решение: 1) Выберем на отрезке А1В т. N, так что A1N=NB=CA1. Соединим N с C1.
2) NC1 – средняя линия  А1ВА. Значит, NC1||AA1 и NC1 =1/2AA1.
3) A1M || NC1 и CA1 =NA1. Тогда по теореме Фалеса CM = MC1. Отсюда А1М – средняя линия А1ВА. Значит, NC1||AA1 и NC1 =1/2AA1.
3) A1M || NC1 и CA1 =NA1. Тогда по теореме Фалеса CM = MC1. Отсюда А1М – средняя линия  NCC1. Тогда A1M=1/2NC1. Пусть А1М=x, x=1/2NC1. Отсюда NC1 =2x. Но NC1=1/2АА1. Тогда АА1=4х. Значит, A1M: АА1=1:4. Или A1M: МА=1:3. Ответ: 1:3. NCC1. Тогда A1M=1/2NC1. Пусть А1М=x, x=1/2NC1. Отсюда NC1 =2x. Но NC1=1/2АА1. Тогда АА1=4х. Значит, A1M: АА1=1:4. Или A1M: МА=1:3. Ответ: 1:3.
|
20. Стороны треугольника равны 51, 85 и 104 см. Проведена окружность, которая касается двух меньших сторон треугольника, а центр ее лежит на большей стороне. На какие части большая сторона треугольника делится центром окружности?

| Дано:  АВС. D- центр окружности. АВ=51 см, ВС=85 см, АС=104 см. Найти:AD, DC.
Решение: Т.к. окружность касается сторон треугольника АВС, то т.D равноудалена от сторон <ABC, т.е. она лежит н6а биссектрисе BD. Следовательно, выполняется равенство АВС. D- центр окружности. АВ=51 см, ВС=85 см, АС=104 см. Найти:AD, DC.
Решение: Т.к. окружность касается сторон треугольника АВС, то т.D равноудалена от сторон <ABC, т.е. она лежит н6а биссектрисе BD. Следовательно, выполняется равенство 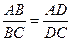 . Пусть AD=x, DC=104 –x. Отсюда . Пусть AD=x, DC=104 –x. Отсюда  . 51(104-х)=85х. Или х=39. Ответ: AD=39 см, DC=65 см. . 51(104-х)=85х. Или х=39. Ответ: AD=39 см, DC=65 см.
|
21. В треугольнике с основанием а и высотой h вписан квадрат так, что две его вершины лежат на основании треугольника, а другие две – на боковых сторонах. Найдите сторону квадрата.

| Дано:  АВС. OMPK- квадрат, АС= а, ВD= h. Найти: MP.
Решение:
1) АВС. OMPK- квадрат, АС= а, ВD= h. Найти: MP.
Решение:
1)  MBP ~ MBP ~  ABC (по двум углам).
Т.к. ABC (по двум углам).
Т.к.  В – общий, <BAC=<BMP (как соответственные при параллельных прямых АС и МР). Из подобия следует: В – общий, <BAC=<BMP (как соответственные при параллельных прямых АС и МР). Из подобия следует: 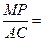  .
2) ВЕ и BD сходственные стороны, тогда .
2) ВЕ и BD сходственные стороны, тогда  . Пусть МР=х, тогда ВЕ=h-x. Т.е. . Пусть МР=х, тогда ВЕ=h-x. Т.е.  . Отсюда . Отсюда  . .
|


 АВС,
АВС,  С =
С =  .
Доказать:
.
Доказать: 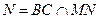 . Получим
. Получим 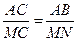 .
4) Из условия задачи имеем
.
4) Из условия задачи имеем 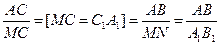 . Или по другому
. Или по другому  . Отсюда А1В1=MN. Следовательно,
. Отсюда А1В1=MN. Следовательно, 
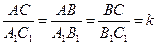 , BH
, BH  AC, B1H1
AC, B1H1 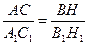 .
Доказательство:
1)
.
Доказательство:
1)  . Но
. Но 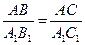 . Тогда
. Тогда 
 .
2)
.
2)  . Т.е. получили, что стороны образующие угол С, пропорциональны. И
. Т.е. получили, что стороны образующие угол С, пропорциональны. И  . И т.к. из подобия треугольников
. И т.к. из подобия треугольников 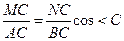 . k = cos<C.
. k = cos<C.

 .
Доказательство:
1) Проведем перпендикуляры СH2 и AH1.
2)
.
Доказательство:
1) Проведем перпендикуляры СH2 и AH1.
2)  . (1)
3) СH2 || AH1.
4)
. (1)
3) СH2 || AH1.
4) 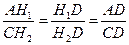 . (2).
5) Из равенств (1) и (2) следует
. (2).
5) Из равенств (1) и (2) следует  .
.

 . (1)
3) В
. (1)
3) В 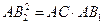 . (2)
4) В
. (2)
4) В 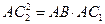 . (3)
5) Из равенств (1), (2) и (3) следует:
. (3)
5) Из равенств (1), (2) и (3) следует:
 . Т.е.
. Т.е.
 . Отсюда
. Отсюда  .
.

 . (1)
2)
. (1)
2)  ABH ~
ABH ~  . (2)
3) Из (1) и (2) следует
. (2)
3) Из (1) и (2) следует 
 .
Отсюда
.
Отсюда 

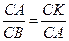 . Отсюда СК=
. Отсюда СК=  . СК=КВ=12-
. СК=КВ=12- 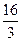 =
=  .
. 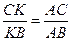 . Отсюда АВ=
. Отсюда АВ= 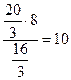 . Ответ: 10.
. Ответ: 10.

 d
d  .
Доказательство:
1)
.
Доказательство:
1) 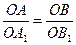 , по теореме о пропорциональных отрезках. Из подобия следует:
, по теореме о пропорциональных отрезках. Из подобия следует: 
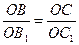 , по теореме о пропорциональных отрезках. Из подобия следует:
, по теореме о пропорциональных отрезках. Из подобия следует:  .
Тогда
.
Тогда  . В каком отношении медиана СС1 делит отрезок АА1?
. В каком отношении медиана СС1 делит отрезок АА1?
 СВ, ВА1:А1С = 2:1, С1
СВ, ВА1:А1С = 2:1, С1 
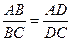 . Пусть AD=x, DC=104 –x. Отсюда
. Пусть AD=x, DC=104 –x. Отсюда  . 51(104-х)=85х. Или х=39. Ответ: AD=39 см, DC=65 см.
. 51(104-х)=85х. Или х=39. Ответ: AD=39 см, DC=65 см.

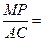
 .
2) ВЕ и BD сходственные стороны, тогда
.
2) ВЕ и BD сходственные стороны, тогда  . Пусть МР=х, тогда ВЕ=h-x. Т.е.
. Пусть МР=х, тогда ВЕ=h-x. Т.е.  . Отсюда
. Отсюда  .
.



