Они представляют собой сердечники, на которые надевают катушки обмотки возбуждения. Сердечники главных полюсов, как и якоря, собирают из отдельных листов стали. Зачем это делают? По катушке сердечника проходит постоянный магнитный поток, а сам сердечник неподвижен и, следовательно, вихревые токи в нем возникнуть не могут. Все это было бы так, если бы якорь имел гладкую поверхность. В действительности зубцы и впадины его сердечника, перемещаясь при вращении под полюсами, искажают магнитное поле и вызывают пульсацию магнитного потока, из-за чего в сердечнике полюса возникают вихревые токи. Вот и приходится набирать сердечник из тонких листов стали, т. е. выполнять шихтованным.
Чтобы обеспечить необходимое распределение магнитного потока по поверхности якоря, сердечнику (рис. 21, а и б) придают довольно сложную Т-образную форму: она определяется соотношением размеров ширины сердечника и его полюсного наконечника, формой воздушного зазора, наличием компенсационной обмотки, условиями размещения и закрепления ее и катушек главных полюсов, способом крепления сердечников к остову.

Тяговые двигатели электровозов постоянного тока имеют две или три пары главных полюсов, а на электровозах переменного тока — три пары полюсов.
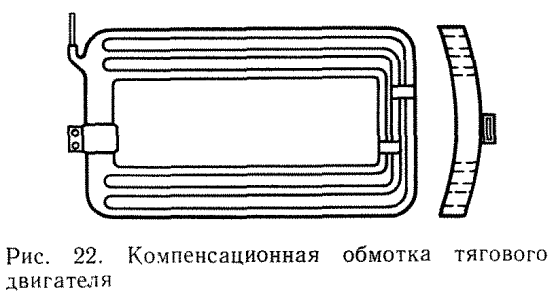
Компенсационная обмотка, применяемая в тяговых двигателях пульсирующего тока и в мощных двигателях постоянного тока, служит для компенсации реакции якоря. Обмотку располагают в пазах наконечника главных полюсов (см. рис. 21, б) и соединяют последовательно с обмоткой якоря. В отечественных тяговых двигателях применена хордовая компенсационная обмотка (рис. 22) из мягкой прямоугольной медной проволоки, выполняемая катушками, которые можно устанавливать и снимать независимо от других обмоток. Крепят компенсационную обмотку в пазах клиньями.