б) Необходимое условие экстремума.
Теорема. Если дифференцируемая функция
Доказательство: Докажем, например, равенство нулю частной производной Частная производная функции Следовательно, Аналогично можно показать, что Эти условия имеют простой геометрический смысл. Они означают, что в точках экстремума касательная плоскость к графику функции Замечание. В точках экстремума хотя бы одна из частных производных может не существовать.
Точки, в которых первые частные производные Из изложенного следует, что точки экстремума функции надо искать в её критических точках.
|
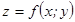имеет в точке 
экстремум, то в этой точке обе частные производные первого порядка равны нулю, т.е.
, 
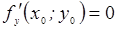
. Рассмотрим в окрестности точки 
только те точки, в которых 
.
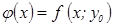, которая имеет экстремум.
. Так как 
, то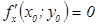 
.
. Необходимые условия определения экстремума переносятся на случай функций нескольких переменных.
.
и 
функции 
