А) Экстремум функции нескольких переменных.
Экстремум функции нескольких переменных. Необходимое условие. а) Экстремум функции нескольких переменных. Обобщим понятия максимума и минимума на случай функции нескольких переменных. Понятия максимума и минимума для функции нескольких переменных вводятся так же, как и для функции одной переменной. Пусть в некоторой области Д задана непрерывная функция Определение. Функция
Точка В точке максимума (минимума) функция достигает наибольшего (наименьшего) значения только по отношению к соседним точкам, т.е. точкам лежащим в некоторой окрестности точки максимума (минимума). Точки максимума и минимума не следует смешивать с точками, в которых функция достигает наибольшего и наименьшего значения в области.
Из определения следует, что если функция
т.е. Если в некоторой окрестности точки Эти условия положения переносятся на функции любого числа переменных. Так же, как и в случае функции одной переменной, возникает вопрос об условиях экстремума.
|

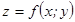
 максимум (минимум), если существует такая окрестность этой точки, что для всех точек
максимум (минимум), если существует такая окрестность этой точки, что для всех точек 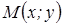 этой окрестности, отличных от
этой окрестности, отличных от  , выполняется неравенство
, выполняется неравенство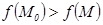
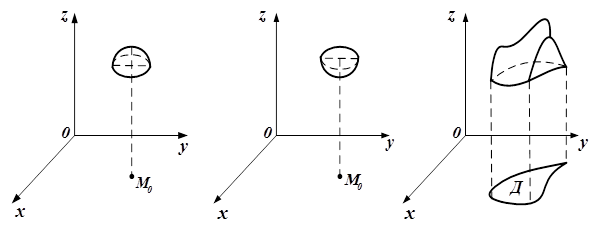
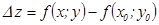 этой функции в точке
этой функции в точке  в случае максимума
в случае максимума в случае минимума,
в случае минимума,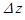 в точках окрестности экстремума не меняет знак.
в точках окрестности экстремума не меняет знак.


