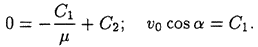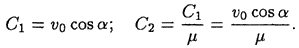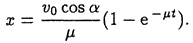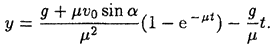Способы решения основных задач динамики точки
В первой основной задаче заданы масса точки Рассмотрим решение этой задачи при координатном способе задания движения. Пусть Oxyz — система декартовых координатных осей; Запишем дифференциальное уравнение движения точки:
Видно, что в этих -уравнениях уже содержится решение задачи в общем виде (для большей убедительности следует поменять местами правые и левые части написанных равенств). В конкретной задаче, дифференцируя заданные функции Пример. Материальная точка М массы
Определить величину силы сопротивления Решение. Движение точки происходит под действием двух сил — собственного веса
Рис. 4. Находим
Подставляя
Таким образом, сила сопротивления пропорциональна первой степени скорости с коэффициентом
Во второй основной задаче задаются масса материальной точки и действующая сила (силы), а определению подлежат уравнения движения точки. В дифференциальных уравнениях движения точки
в этом случае правые части заданы, а искомыми являются функции времени Для того чтобы найти эти функции, требуется выполнить интегрирование дифференциальных уравнений движения при определенных, заданных начальных условиях:
Обычно принимается Пример. Найти уравнения движения материальной точки в примере 1 на с. 9. Решение. Дифференциальные уравнения движения, которые были получены выше на с. 10, запишем в виде:
Точка движется, оставаясь все время в плоскости
Уравнения оказались независимыми, поэтому могут интегрироваться отдельно. Решим вначале первое уравнение, которое в переменной
Это дифференциальное уравнение первого порядка с разделяющимися переменными. После разделения переменных уравнение запишется так:
Теперь можно брать интегралы от обеих частей:
после чего, учитывая, что
где Решаем это логарифмическое уравнение относительно
Далее, заменяя
Снова разделяя переменные и интегрируя, получаем выражение
в котором Это и есть общее решение дифференциального уравнения Постоянные интегрирования определяем по начальным условиям движения. Для этого начальные условия
Из них находим:
Теперь все готово и остается лишь записать уравнение движения
Второе дифференциальное уравнение движения интегрируется по той же общей схеме, что и первое. После интегрирования, которое предлагаем читателю выполнить самостоятельно, получаем второе уравнение движения
|

 и ее закон движения в той или иной форме — векторной, координатной или естественной. Требуется найти неизвестную силу, действующую на движущуюся точку.
и ее закон движения в той или иной форме — векторной, координатной или естественной. Требуется найти неизвестную силу, действующую на движущуюся точку. — заданные уравнения движения точки в этих осях. Неизвестную равнодействующую F сил, приложенных к точке, будем искать, определяя ее проекции
— заданные уравнения движения точки в этих осях. Неизвестную равнодействующую F сил, приложенных к точке, будем искать, определяя ее проекции  на координатные оси.
на координатные оси.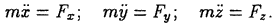
 два раза по времени и подставляя результат в дифференциальные уравнения движения, определяем проекции
два раза по времени и подставляя результат в дифференциальные уравнения движения, определяем проекции  искомой равнодействующей. Далее, если это необходимо, определяем модуль силы и косинусы углов, образуемых силой с координатными осями.
искомой равнодействующей. Далее, если это необходимо, определяем модуль силы и косинусы углов, образуемых силой с координатными осями. падает вертикально в среде с сопротивлением, причем уравнение движения имеет вид (рис. 4):
падает вертикально в среде с сопротивлением, причем уравнение движения имеет вид (рис. 4):
 .
. и силы сопротивления -
и силы сопротивления -  ; проекция равнодействующей на направление движения (ось у) будет равна
; проекция равнодействующей на направление движения (ось у) будет равна  . Составляем дифференциальное уравнение движения (при прямолинейном движении имеет место одно дифференциальное уравнение движения):
. Составляем дифференциальное уравнение движения (при прямолинейном движении имеет место одно дифференциальное уравнение движения):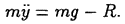
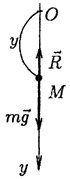
 , для чего дважды дифференцируем по времени заданный закон движения точки:
, для чего дважды дифференцируем по времени заданный закон движения точки:
 в дифференциальное уравнение движения и разрешая его относительно неизвестной R, получаем:
в дифференциальное уравнение движения и разрешая его относительно неизвестной R, получаем:
 . Векторная формула для силы будет иметь вид
. Векторная формула для силы будет иметь вид
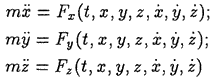
 , определяющие закон движения точки.
, определяющие закон движения точки.
 .
.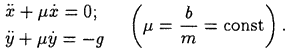
 , поэтому имеем не три, а только два дифференциальных уравнения движения. Для решения задачи требуется проинтегрировать эти уравнения при следующих начальных условиях:
, поэтому имеем не три, а только два дифференциальных уравнения движения. Для решения задачи требуется проинтегрировать эти уравнения при следующих начальных условиях:
 можно представить в следующем виде:
можно представить в следующем виде: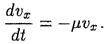
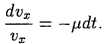

 , получаем:
, получаем:
 — произвольная постоянная интегрирования.
— произвольная постоянная интегрирования. :
:
 выражением
выражением  , снова приходим к дифференциальному уравнению с разделяющимися переменными
, снова приходим к дифференциальному уравнению с разделяющимися переменными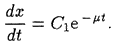
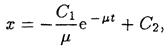
 — новая (вторая) постоянная интегрирования. (Заметим, что
— новая (вторая) постоянная интегрирования. (Заметим, что  представляют собой разные формы записи одной и той же (первой) постоянной интегрирования).
представляют собой разные формы записи одной и той же (первой) постоянной интегрирования). . Для того чтобы найти уравнение движения точки, требуется найти постоянные интегрирования
. Для того чтобы найти уравнение движения точки, требуется найти постоянные интегрирования  и подставить в это общее решение.
и подставить в это общее решение. подставляем в выражения для
подставляем в выражения для  , что дает нам два уравнения (конечных, не дифференциальных) для определения
, что дает нам два уравнения (конечных, не дифференциальных) для определения  :
: