Коливальна ланка

2 1

kx_вх х_вих=kx_вх

1 1

0 t 0 t

а г

х_вих х_вих

х_вх 2 ∞;

kх_вх

1 1

0 t 0 t

Б д

x_вих с

х_вх

х_вих=f(t) i

u_c

х_вх=f(t) u_вх R u_вих

arctgk

0 t

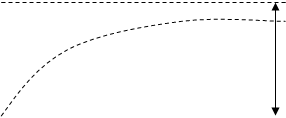
В e

мал.2.1. Перехідні процеси в ланках:

а – аперіодичній; б – коливальній; в – інтегруючій; г – підсилюючій; д - ідеальній диференціюючій; е - схема диференціюючої ланки

Розв’язуючи рівняння (2.2) відносносно хвих(t), отримаємо

xвих(t) = kxвх (1 – e^-t/T) (2.4)

або при хвх = 1 маємо перехідну функцію аперіодичної ланки:

h(t) = k (1 – e^-t/T) (2.5)

 

Графік перехідного процесу в аперіодичній ланці зображений на мал. 2.1, а кривою 1. Як видно з рівняння (2.4) та мал. 2.1, а, перехідний процес в аперіодичній ланці повністю визначається значеннями коефіцієнта підсилення ланки k та її постійної часу Т.

Якщо диференційне рівняння аперіодичної ланки має вигляд

Тdxвих/dt – xвих = kxвх (2.6)

то перехідний процес в ній описується рівнянням

xвих(t) = ke^t/T (2.7)

 

і задається кривою 2 на мал. 2.1, а. Ланка, яка описується рівнянням (2.6), називається нестійкою аперіодичною ланкою.

Аперіодичні ланки в лінійних динамічних системах зустрічаються дуже часто. Наведемо деякі приклади.

Приклад 1. Нехай до обмотки ОВГ (мал. 1.6, а) поданий скачок напруги u_в. Диференційне рівняння ланки, що розглядається, має вигляд

 

u_в = i_вR_в + Ldi_в/dt або u_в/R_в = i_в + Tdi_в/dt,

 

де T=L/R_в – постійна часу ланцюга ОВГ: L – індуктивність ланцюга; R_в – опір ланцюга.

Враховуючи, що в ланці що розглядається i_в =x _вих, u_в=x_вх, отримуєм

 

Tdx_вих/dt + x_вих = kx_вх,

де k = x_вих / x_вих = 1 / R_в - коефіцієнт підсилення.

Приклад 2. Якщо в схемі (мал. 1.6, б) розглянути зв’язок між змінними ω та і, то, використовуються електромеханічні властивості системи що розглядається при умові пропорційності між ω та М_с – моментом опору на валу електродвигуна, можна отримати

 

Тdω/dt + ω = ki,

 

де Т = І/с₁ – постійна часу; І – момент інерції, приведений до валу двигуна; с₁ коефіцієнт пропорційності між М_с і ω; k=k_м/с₁ – коефіцієнт підсилення; k_м - коефіцієнт пропорційності між момементом М, який розвивається двигуном, та струмом і.

 

Коливальна ланка

Коливальною називається ланка, в якій зв’язок між вихідною та вхідною величинами виражається рівнянням

 

Т² d²x_вих/dt² +2ξTdx_вих/dt + x_вих = kx_вх (2.8)

 

при умові ξ < 1. У рівнянні (2.8) Т – постіна часу; k – коефіцієнт підсилення; ξ – коефіцієнт затухання.

Розв’язок диференційного рівняння (2.8), а отже, характер зміни х_вих(t) залежить від значення коренів відповідного характеристичного рівняння

 

Т²α² + 2ξТα + 1 = 0; (2.9)

α_1,2 = - 1/Т (ξ + √ξ² - 1). (2.10)

 

При ξ < 1 корені α₁ та α₂ – комплексні. В цьому випадку перехідний процес в ланці носить коливальний характер, а перехідна функція коливальної ланки має вигляд

 

h(t)=k[1-(e^-ξt/T/√1-ξ²) sin((√1-ξ²/T) *t+arctg(√1-ξ²/ξ))] (2.11)

 

Коливання (2.11) носять затухаючий характер – крива 1 на мал. 2.1 б. Дійсно, з (2.11) при t→ ∞ маємо х_вих(t) → k.

Застосовуючи до рівняння (2.8) перетворення Лапласа при нульових початкових умовах, отримаємо передаточну функцію стійкої коливальної ланки:

 

W(p) = x_вих(p)/x_вх(p) = k/(T²p² + 2ξTp + 1) (2.12)

 

Якщо диференційне рівняння ланки має вигляд

 

Т²d²x_вих/dt² – 2ξdx_вих/dt + x_вих = kx_вх, (2.13)

 

то перехідна функція

h(t) = k(e^ξt/T/√1-ξ²)sin((√1-ξ²/T)t+arctg(√1-ξ²/ξ)). (2.14)

 

З (2.14) при t→ ∞ слідує h(t)→ ∞, тобто коливання в такій ланці носять розбіжний характер (крива 2 на мал.2.1, б). Ланка, в якій зв’язок між вхідною та вихідною величинами описується диференційним рівнянням (2.13) при ξ < 1, називається нестійкою коливальною ланкою.

Нарешті, якщо в рівнянні (2.8) ξ >1, то корені характерестичного рівняння (2.9) будуть дійсними:

 

α₁ = - (ξ + √ξ² - 1)/T α₂ = -(ξ - √ξ²-1)/Т