Побудова параметричних схем математичних моделей
Таблиця 1
Для рішення кожного виду приведеного рівняння використовуються відомі числові методи рішення з розробленими для них алгоритмами. Кожен вид рівняння використовується для опису специфічної інженерної задачі.
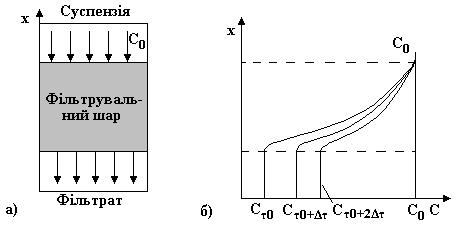
Еліптичне рівняння характеризує об’єкт, який описує, в двох координатній системі простору. При цьому опис виконується для статичних об’єктів, де змінна часу відсутня. Модель дає змогу дослідити розподіл основного параметра у двох координатному просторі. Рис. 4.1. Приклади використання моделі еліптичного типу
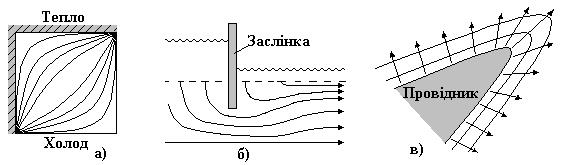
Прикладом з теплообміну може бути підігрівання пластини з двох боків, або охолодження ребра холодильника (рис. 4.1.а). Модель дає змогу визначити розподіл температур по зоні, температурний потенціал і відтік тепла від зони нагрівання до зони охолодження. Еліптичне рівняння також дає змогу описати потік рідини навколо заслінки, або в зоні звуження, потенціал електричного поля біля провідника (рис. 20б і в), концентрацію сухих речовин суспензії по перетині фільтра та ін. Параболічне рівняння на відміну від рівняння еліптичного типу вказує як основний параметр моделі змінюється одночасно в часі і просторі.
Простим прикладом використання цієї моделі є визначення розподілу температури вздовж тонкого металевого стержня закріпленого з двох боків. На кінці стержня подається фіксована температура. В цьому випадку є тільки одна координата простору – довжина. Вважається, що у всіх точках на перетині стержня температура однакова. Рішенням задачі є зміна температурного стану по довжині стержня на протязі деякого часу. На рис. 21 показано а) - схема стержня і б) – криві зміни температури по довжині стержня в різні моменти часу. Рис. 4.2. Динаміка розподілу температур в параболічній моделі
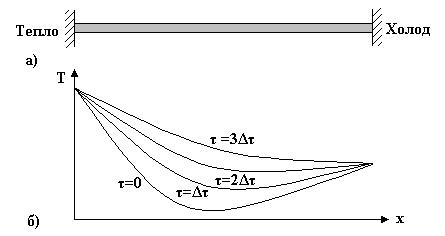
Подібні рівняння можуть бути використані при моделюванні інших процесів, наприклад, процесу фільтрування соку через шар осаду (рис. 4.3). Рис. 4.3. Динаміка зміни концентрації на фільтрі в параболічній моделі
Процес фільтрування описується рівнянням Дарсі:
де х - координата вздовж фільтрувального шару, С - концентрація твердих частинок в суспензії, D - коефіцієнт дифузії. На рис. 4.3.б показана динаміка зміни концентрації твердих частинок в суспензії вздовж фільтрувального шару. Гіперболічні рівняння є диференційними рівняннями другого порядку по часу з частинними похідними. Ними описуються коливання різних хвиль. Прикладом такого є рівняння, яке описує коливання струни. До моделей, які можуть описуватись гіперболічним рівнянням відносяться моделі мостів і балок під час розгойдування, хвильові потоки води, коливання електричних імпульсів та ін.
4.3.Рішення диференційних рівнянь другого порядку в частинних похідних
Розв’язання диференційних рівнянь другого порядку в частинних похідних виконується методом кінцевих різниць. Для цього апарат, або технологічний об’єкт розбивається на зони. Розглянемо цей метод на прикладі розв’язання параболічної моделі тонкого стержня, який нагрівається з одного боку (рис. 4.4). Ця модель описується відомим рівнянням (4.7)
Розіб’ємо умовно стержень на n зон з довжиною зони Dх = х/n, де х - довжина стержня. Допустимо, що кожна зона це об’єкт із зосередженими параметрами і температура у всіх точках і-ї зони Ті рівна. Між зонами відбувається теплообмін. Параметрична схема передачі тепла між зонами показана на рис. 4.4в. Розглянемо процес теплообміну між зонами на прикладі і-ї зони. Передача тепла від і-1-ї до і-ї зони записується рівнянням теплового потоку:
а від і+1-ї до і-ї зони рівнянням теплового потоку:
Складемо рівняння теплового балансу в і-й зоні, вважаючи, що тепло зони дорівнює:
В динамічному режимі це буде описано диференційним рівнянням:
яке після спрощення матиме вигляд:
де: lі - коефіцієнт теплопровідності, rі - питома вага стержня, Сі - коефіцієнт теплоємкості, S - площа поперечного перетину стержня. Склавши рівняння теплового балансу для кожної і-ї зони, де і= 1,..,n, отримаємо систему із n диференційних рівнянь першого порядку, яка розв’язується відомими методами, наприклад методом Рунге-Кутта.
Розв’язання задачі з еліптичною моделлю, де основний параметр змінюється по двох просторових координатах виконується подібно. Просторовими координатами моделі можуть бути довжина і висота апарату - х, у (рис. 4.5а) або довжина і радіус апарату - х і R (рис. 4.5б). Рис. 4.5. Розбиття об’єкту, що описаний еліптичною моделлю, на зони Такі моделі виникають при дослідженні зміни кривої швидкості потоку у апараті (рис. 4.5.а) або зміни концентрації продукту в циліндричному апараті (рис. 4.5.б). Побудова параметричних схем математичних моделей
Параметричні схеми математичних моделей показують внутрішню наповненість математичної моделі, ті формули, якими описаний зв’язок між вхідними і вихідними параметрами. В них відображена послідовність обчислення проміжних змінних моделі і зв’язок формул між собою. Тут показані причинно-наслідкові зв’язки між змінними, які відображають механізм фізичних і хімічних явищ технологічного процесу. Правильно складена параметрична схема моделі дає змогу легко скласти алгоритм обчислення моделі, який при використанні ітераційних обчислювальних циклів має збіжність і дає правильний результат.
4.4.1. Моделювання гідродинаміки в ємності з рідиною
Розглянемо ємність в яку поступає G1 і з якої витікає рідина G2 (рис. 4.6а). Розглянемо просту задачу визначення рівня рідини в ємності в любий момент часу t. На основі рівняння матеріального балансу можна записати, що швидкість накопичення рідини в ємності дорівнює різниці між рідиною яка поступає і витікає:
а так як площа поперечного перетину ємності S постійна, то об’єм рідини дорівнює:
Параметрична схема математичної моделі матиме вигляд показаний на рис. 4.6б. Тут S – вхідний параметр, h - вихідний, а G1, G2 - параметри керування.
Зробимо модель більш складнішою. Будемо вважати, що потік рідини з витратами G1 проходить до ємності через кран із середовища з тиском Р1, і поступає з витратами G2 також через кран в середовище з тиском Р3 (рис. 4.7а). В ємності, біля місця де поступає рідина, тиск залежить від рівня рідини в ємності h і атмосферного тиску Р0 і дорівнює Р2: Р2 = Р0 + rh, (4.17) де r - густина рідини. Значення витрат рідини будемо рахувати по формулах:
де k1 i k2 - коефіцієнти можливостей пропускання кранами. Параметрична схема вдосконаленої математичної моделі представлена на рис. 4.7б. Тут показана послідовність обчислень змінних в моделі і взаємозв’язок між формулами. Вхідними параметрами моделі є: S, r, k1 i k2, вихідними: G1, G2, h i P2, а параметрами керування: Р1, Р3, і Р0.
впливу рівня рідини на витрати
Можливий випадок використання герметичної ємності. Тоді тиск над поверхнею Р0 буде змінюватись в залежності від рівня рідини в ємності (рис. 4.8а). Якщо вважати, що газ в ємності підкорюється закону для ідеальних газів, тоді:
де R - універсальна газова постійна, Vг - об’єм, Тг - температура і М - маса газу. Якщо зробити припущення, що процес розширення або стискування газу проходить ізотермічно при Тг = const, тоді об’єм газу буде дорівнювати: Vг = V0 - Sh, (4.20) де V0 - об’єм ємності. На рис. 4.8б показана вдосконалена параметрична схема математичної моделі гідравлічної ємності з урахуванням її герметичності. До вхідних параметрів добавились змінні: V0, M, R, Tг , до вихідних проміжна величина: Vг, а параметр керування Р0 став вихідним параметром, тому що обчислюється в межах моделі.
4.4.2. Моделювання теплообміну в ємності ідеального змішування з підігріванням Гідродинамічну математичну модель ємності можна доповнити моделлю теплообміну. На рис. 4.9а показана ємність з паровою сорочкою, де тиск пари регулятором тиску підтримується постійним. Матеріальний баланс в ємності описується вже раніше приведеним рівнянням (4.15). Тепловий баланс описується аналогічно матеріальному рівнянням:
Рис. 4.9. Параметрична схема моделі теплообміну в ємності ідеального змішування
Після підстановки приведених рівнянь формула (4.21) запишеться:
де: Т1, Т2, Тп - відповідно температура рідини на вході, в ємності і пари, С - теплоємність рідини, r - густина рідини, k - загальний коефіцієнт теплопередачі, V - об’єм рідини в ємності. Температура пари в паровій сорочці є функцією тиску пари Рп. Запишемо цю відому залежність в загальному вигляді: Тп =f(Pп). Тиск пари підтримується на необхідному рівні регулятором тиску. По приведеним рівнянням складемо параметричну схему математичної моделі об’єкту (рис. 4.9б). Вхідними параметрами моделі будуть: F, С, r, k, вихідними: Т2, Тп, Qп і V, а параметрами керування: G1, G2, Т1, Pп. Таке розташування рівнянь в параметричній схемі моделі дає змогу послідовно обчислити матеріальний баланс моделі і визначити об’єм рідини в ємності V, із рівняння теплопередачі визначити тепло Qп, яке передається від пари до рідини, і із теплового балансу визначити температуру в ємності Т2. Значення температури пари в залежності від тиску може бути описане у вигляді функції, або апроксимоване по даних таблиці.
|

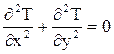



 , (4.9)
, (4.9)
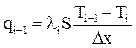 , (4.10)
, (4.10)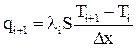 (4.11)
(4.11)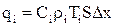 (4.12)
(4.12)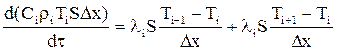 , (4.13)
, (4.13) , (4.14)
, (4.14)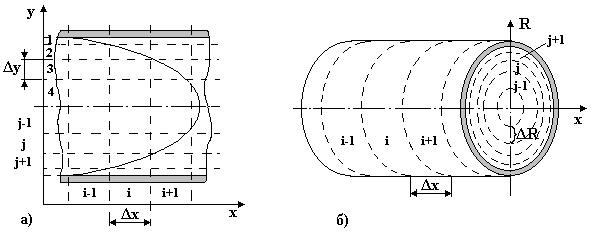
 , (4.15)
, (4.15)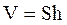 , де h - рівень рідини. Враховуючи останнє, рівняння (4.15) запишемо:
, де h - рівень рідини. Враховуючи останнє, рівняння (4.15) запишемо: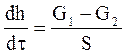 (4.16)
(4.16)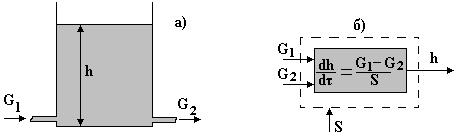
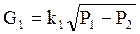
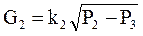 , (4.18)
, (4.18)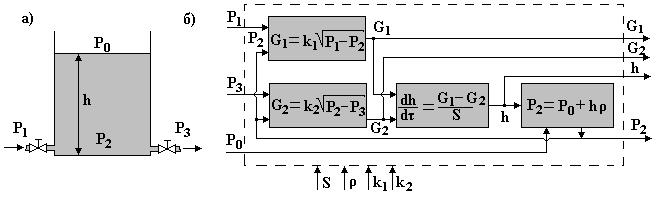
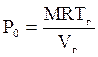 , (4.19)
, (4.19)
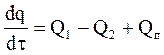 , (4.21)
, (4.21)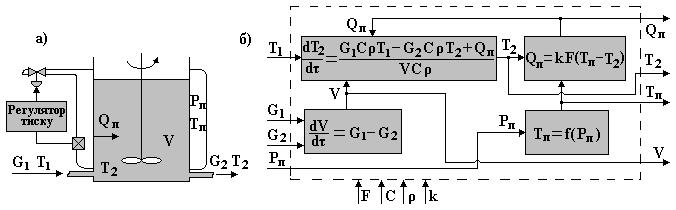
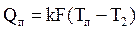 . (4.22)
. (4.22)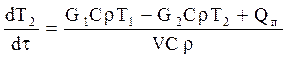 , (4.23)
, (4.23)


