Допущения при расчете по этому методу

1. Линейная зависимость между напряжениями и деформациями.

2. Осадки рассматриваются, исходя из max P_z – под центром фундамента.

3. Не учитывается, как правило, слоистость напластований при построении P_z.

4. Это задача пространственная (6 компонентов напряжений), мы учитываем только P_z (5 комп. не учитываем).

5. Не учитываем боковое расширение грунта.

6. На некоторой глубине ограничиваем активную зону, ниже которой считаем, что грунт практически не деформируется.

 

 

Определение осадки фундамента по методу эквивалентного слоя
(Н. А. Цытович, 1934 год)

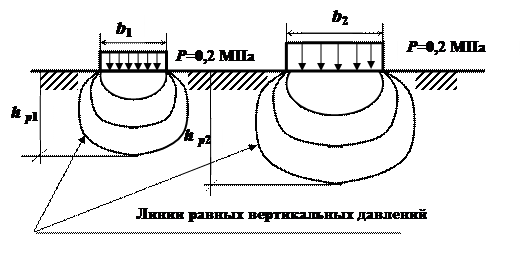
Рис. 5.7. Эпюры распределения давлений при различной площади загрузки

 

При большей площади загрузки глубина распределения давлений и объем грунта, подвергающийся деформации, будут больше. Следовательно, и осадки будут больше.

Под эквивалентным слоем подразумевается некоторый ограниченный по толщине слой грунта, который при сплошной, равномерно распределенной нагрузке, приложенной к границе основания, дает значение осадки, равное осадке фундамента, имеющего ограниченные размеры в плане при той же нагрузке и аналогичных грунтовых условиях. Другими словами, в данном методе пространственная задача расчета осадок может заменяться одномерной.

В случае однородного основания грунт моделируется сплошным линейно деформируемым телом. Считается, что осадка основания определяется всеми компонентами напряжений и зависит от жесткости фундамента. Учитывается также боковое расширение грунта основания.

В методе эквивалентного слоя конечную осадку фундамента определяют в результате решения задачи теории упругости о деформировании упругого полупространства под действием равномерно распределенной нагрузки по формуле

 

s = h_e∙m_v∙p ₀, (5.5)

 

где m_v – коэффициент относительной сжимаемости грунта;

p ₀ – дополнительное давление по подошве фундамента;

h_e – мощность эквивалентного слоя грунта:

 

h_e = A∙ω∙b, (5.6)

 

b – ширина подошвы фундамента; ω; – коэффициент, зависящий от формы подошвы и жесткости фундамента; А – коэффициент, зависящий от коэффициента бокового расширения грунта ν:

A = (1– ν;)²/(1–2 ν;). (5.7)

 

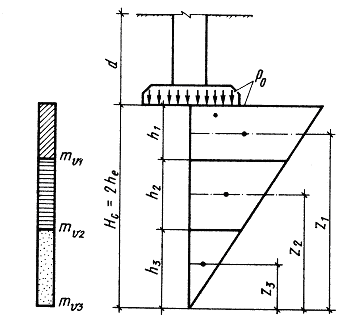
Произведение A∙ω называют коэффициентом эквивалентного слоя, который находят по табличным данным.

Метод эквивалентного слоя позволяет определять осадку слоистого основания с использованием приближенного решения.

Так, в расчетной схеме сжимаемую толщину основания, влияющую на осадку фундамента, принимают равной H_c = 2 h_e, а распределение дополнительных вертикальных напряжений – по треугольной эпюре (рис. 5.8, а). Вершину треугольной эпюры напряжений назначают на глубине Н_с, а основание эпюры р ₀ – под подошвой фундамента. Грунты, находящиеся в пределах глубины сжимаемости толщи, считаются однородными с осредненными характеристиками.

Осадку слоистого основания также вычисляют по формуле (5.5), с той лишь разницей, что в ней используют средний коэффициент относительной сжимаемости, определяемый из условия, что в пределах сжимаемой толщи полная осадка равна сумме осадок, входящих в нее слоев. Средний коэффициент относительной сжимаемости находят из выражения

 

, (5.8)

 

где h_i – высота i -го слоя грунта в пределах сжимаемой толщи;

m_vi – коэффициент относительной сжимаемости i -го слоя;

z_i – расстояние от нижней точки треугольной эпюры до середины i-го слоя (рис. 5.8).

Метод эквивалентного слоя позволяет рассчитывать осадку с учетом влияния других, рядом расположенных фундаментов с помощью метода угловых точек, о котором уже говорилось выше.

 

Рис. 5.8. Расчетная схема к методу эквивалентного слоя при слоистом пластовании грунтов