Деформации ползучести грунта при уплотнении
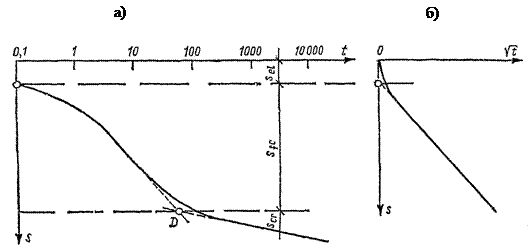
Если деформацию образца водонасыщенного грунта в одометре или осадку слоя грунта без возможности бокового расширения изобразить во времени кривой в полулогарифмической системе координат, то она будет иметь вид, показанный на рис. 5.13, а.На этой кривой можно выделить три основных участка, соответствующих трем слагаемым осадки: преимущественно упругой (начальной) осадке sei, развивающейся до начала фильтрационной консолидации; осадке sf.c,обусловленной фильтрационной консолидацией, и осадке scr, развивающейся вследствие ползучести грунта. Осадку, развивающуюся после фильтрационной консолидации, обычно называют осадкой вторичной консолидации. Фактически деформации ползучести, развивающиеся с момента приложения нагрузки, составляют небольшую долю sf.c в период развития фильтрационной консолидации, поэтому их можно не выделять.
Рис. 5.13. Кривые нарастания деформаций (осадок) во времени
Начальную (преимущественно упругую) осадку можно найти по графику, построенному в координатах s и √ t (рис. 5.13, б). Нарастание во времени относительной деформации неводонасыщенных грунтов может быть, как считает Н. А. Цытович, установлено по теории наследственной ползучести. В таком случае уравнение напряженно-деформированного состояния грунтов при затухающей ползучести и при непрерывном одноосном загружении или одномерном уплотнении различным давлением (переменным или постоянным) в момент времени tбудет иметь вид
где Eel – мгновенный модуль деформации скелета грунта; σ;(t)и σ;(t 0) – напряжения, развивающиеся соответственно к моментам времени t и t 0; t – текущая координата времени; t 0 – момент времени, соответствующий приложению нагрузки, вызывающей напряжение σ;(t 0), которое действует в течение отрезка времени dt 0.
где Уравнение (5.14) свидетельствует о зависимости полной деформации скелета грунта, обладающего ползучестью, не только от напряженного состояния, но и от предыстории нагружения в момент времени t0. Этим обусловлено название теории – теория наследственной ползучести. Ядро ползучести для дисперсных грунтов часто представляют в виде простейшей зависимости, подтверждаемой экспериментами:
где δ; и δ;1 – параметры ползучести, определяемые по результатам опытов. Для нахождений δ;1 после окончания фильтрационной консолидации (начиная с момента времени tf.c)строят графическую зависимость, показанную на рис. 5.14, где
Параметр ползучести δ; можно определить по формуле
где Величину
где Когда деформации ползучести в период фильтрационной консолидации можно считать незначительными,
здесь Sel и Sf.с определяются по графику (см. рис. 5.13); h – высота образца; Значение
где Таким образом, по результатам экспериментов определяют все параметры, необходимые для нахождения относительной деформации ползучести однофазного грунта, что дает возможность составлять прогноз деформаций ползучести грунтов. В двухфазных грунтах одновременно развиваются деформации ползучести, фильтрационной консолидации и изменения объема пузырьков воздуха в поровой воде по мере изменения в ней давления. Решения для ряда таких задач освещены в трудах Н. А. Цытовича, Ю. К. Зарецкого, З. Т. Тер-Мартиросяна и др. Однако при приближенных расчетах осадки во времени относительно хорошо фильтрующих грунтов (суглинков или глин с прослоями песка) используют раздельное определение развития осадок во времени в результате сжатия поровой воды, фильтрационной консолидации и ползучести с применением графика развития деформаций во времени (см. рис. 5.13). В таком случае кривую нарастания осадки во времени в период деформаций ползучести заменяют прямой, начиная от точки D.
Вопросы нелинейной механики грунтов Ранее отмечалось, что близкая к линейной зависимость при небольших давлениях наблюдается в пределах фазы упругих деформаций и фазы уплотнения и местных сдвигов. Если давление по подошве жестких фундаментов не вызывает развития интенсивных деформаций сдвигов (пластических деформаций), то, как показано ранее, осадку сооружений с успехом можно рассчитывать исходя из линейной зависимости между напряжениями и деформациями. В ряде случаев осадка, полученная при таком расчете, оказывается существенно меньше предельно допустимого значения. Однако увеличить давление по подошве рассчитываемых фундаментов на основе линейной механики грунтов нельзя, так как при повышенных давлениях нарушается принятая в расчетах линейная зависимость. Нарушение линейной зависимости между давлением и осадками жесткого фундамента можно объяснить значительным развитием деформаций сдвигов и изменением объема грунта не только в зависимости от суммы главных напряжений, но и от соотношения между главными и касательными напряжениями (явления контракции и дилатансии). В таком случае приходится рассматривать напряженное состояние грунтов, например, по октаэдрическим площадкам, равнонаклонным к плоскостям, по которым действуют главные напряжения. Согласно решениям общей механики сплошных сред, на эти площадки будут действовать октаэдрические напряжения: Нормальные
касательные
Кроме деформаций объема, существенное значение имеют деформации формы.
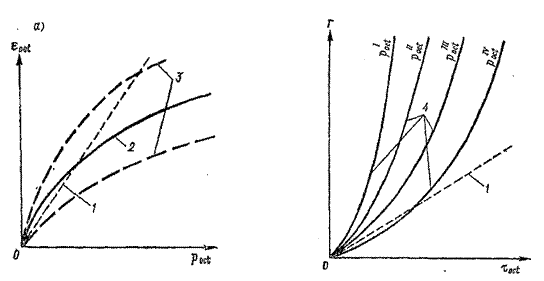
где γ;1, γ;2, γ;3 – наибольшие (главные) деформации сдвигов. Деформации объема и формы могут быть выражены через σoct и τoct. На рис. 5.15, а показано изменение относительной октаэдрической деформации (изменения объема) εoct при увеличении σoct = poct. Линия 1 соответствует линейной зависимости между напряжениями и деформациями; линия 2 – экспериментальная кривая для случая неизменности объема при действии касательных напряжений; линии 3 – экспериментальные кривые, полученные при изменении объема в результате деформации сдвигов. На рис. 5.15, б представлена зависимость меры деформаций формы Г от τoct при различных октаэдрических нормальных напряжениях. Здесь также линия 1 отражает линейную зависимость между напряжениями и деформациями. Кривые 4 соответствуют развитию меры деформаций формы при различных октаэдрических нормальных напряжениях.
Рис. 5.15. Графики зависимости деформаций:
Анализируя эти графики, следует отметить, что линейную зависимость между напряжениями и деформациями можно использовать при сравнительно небольших октаэдрических нормальных и касательных напряжениях. При больших значениях этих напряжений надо учитывать нелинейную зависимость между напряжениями и деформациями грунтов. Это необходимо при возведении, например, тяжелых сооружений (плотин, атомных реакторов и др.), передающих на грунт давление, существенно большее его расчетного сопротивления, при котором еще обеспечивается линейная зависимость между напряжениями и деформациями. Решения нелинейной механики грунтов позволяют рациональнее проектировать основания сооружений, сложенные сравнительно малосжимаемыми грунтами. В таком случае требуются определение с высокой точностью сравнительно большого числа параметров деформируемости грунта и ведение расчетов с помощью ЭВМ методом итерации.
|

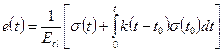 , (5.10)
, (5.10)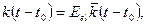 (5.11)
(5.11)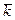 ∙(t – t 0) – ядро ползучести, характеризующее скорость деформации ползучести при постоянном напряжении, отнесенную к его единице.
∙(t – t 0) – ядро ползучести, характеризующее скорость деформации ползучести при постоянном напряжении, отнесенную к его единице.
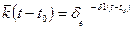 , (5.12)
, (5.12)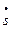 – скорость осадки;
– скорость осадки;  . (5.13)
. (5.13)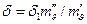 , (5.14)
, (5.14)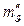 – коэффициент относительной сжимаемости вследствие ползучести грунта, определяемый на конец опыта;
– коэффициент относительной сжимаемости вследствие ползучести грунта, определяемый на конец опыта; 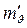 – коэффициент относительной сжимаемости вследствие упругих деформаций образца и фильтрационной консолидации.
– коэффициент относительной сжимаемости вследствие упругих деформаций образца и фильтрационной консолидации.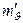 находят по формуле
находят по формуле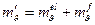 , (5.15)
, (5.15)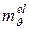 – коэффициент относительной сжимаемости в период упругих деформаций;
– коэффициент относительной сжимаемости в период упругих деформаций;  – коэффициент относительной сжимаемости за период фильтрационной консолидации.
– коэффициент относительной сжимаемости за период фильтрационной консолидации.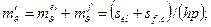 (5.16)
(5.16)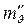 устанавливают по формуле
устанавливают по формуле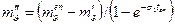 , (5.17)
, (5.17)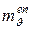 – коэффициент относительной сжимаемости грунта при условной стабилизации образца грунта за период времени ten (на конец опыта).
– коэффициент относительной сжимаемости грунта при условной стабилизации образца грунта за период времени ten (на конец опыта).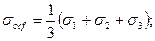 (5.18)
(5.18)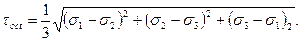 (5.19)
(5.19)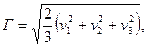 (5.20)
(5.20)