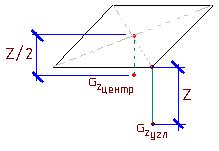
Метод угловых точек. В результате сравнения численных решений оказалось, что напряжение под центром и под углом площади связанны следующим образом:
В результате сравнения численных решений оказалось, что напряжение под центром и под углом площади связанны следующим образом: σzугл/Z=0.25 σzцентр/(0,5z) Для определения вертикального напряжения σz в любой точке полупространства можно воспользоваться выражением σz=0.25αP, где α- коэфф., принимаемый в зависимости от отношения сторон площадей загружения a,b и глубины z.
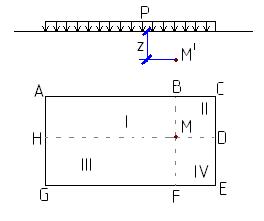
Если проекция рассматриваемой точки M’ на горизонтальную поверхность полупространства (точка М) располагается в пределах площади загружения, то эту площадь можно разбить на 4 прямоугольника (ABMH, BCDM, DEFM, FGHM) так, что бы точка M была угловой точкой каждого из них. Тогда напряжение σz найдем суммированием напряжений под угловыми точками четырех площадей загружения: σz= σz1+ σz2 + σz3 + σz4=0,25(α1+α2 +α3 +α4)P Так, пользуясь методом угловых точек, можно найти напряжение в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади.
|