Распределение напряжений в грунте по подошве сооружений и конструкций конечной жесткости
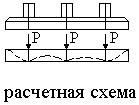
Гибкие фундаменты - это фундаменты, деформации изгиба которых имеют тот же порядок, что и осадки этого же фундамента. (ленточные фундаменты большой длины, загруженные на значительных расстояниях, балки на грунте, большинство плитных фундаментов). Таким образом, при расчёте гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки. При расчёте ленточных фундаментов, загруженных неравномерно сосредоточенными силами необходимо учитывать изгиб в продольном направлении. Вследствие изгиба фундамента конечной жёсткости, давление на грунт увеличивается в местах передачи фундаменту сосредоточенных сил и уменьшается в промежутках между этими силами (см. расчётную схему).
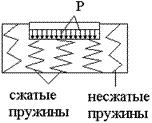
Принципиальная расчётная схема деформирования гибкого фундамента на упругом основании. Теория местных упругих деформаций. Данная теория получила название автора: Фусса-Винклера и была им предложена ещё в 1868 г. Основная предпосылка этой теории – прямая пропорциональность между давлением и местной осадкой. Основание в данном случае может быть представлено в виде системы пружин не связанных между собой (см. схему). В результате под загруженной балкой пружины будут испытывать сжатие, а за пределами балки – находиться в не сжатом состоянии.
Схема модели основания для расчёта гибкой конструкции на упругом основании по методу местных упругих деформаций. Тогда давление основания под загруженной балкой, может быть определено из следующего выражения:
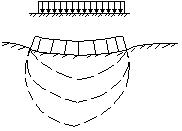
где Px – давление на подошве фундамента; Сz – коэффициент упругости основания (коэффициент постели); Zx – упругая осадка грунта в месте приложения нагрузки. Эта модель хорошо отражает работу конструкции, если основание представлено жидкостью. Поэтому чаще всего этот метод используется при строительстве на слабых грунтах или в случае малой мощности слоя сжимаемого грунта. Следует подчеркнуть, что модели соответствующие гипотезе Фусса-Винклера не в состоянии учитывать разновидность оснований (изменение Ео по глубине и в плане сооружения). В действительности результаты непосредственных наблюдений показали, что оседает не только нагруженная поверхность, но и соседние участки грунта (см. схему).
Схема деформации основания и гибкой фундаментной балки по результатам эксперимента. Грунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория – общих упругих деформаций.
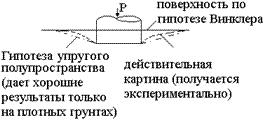
В основу этой теории положено предположение, что грунт является однородным и изотропным. Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости. Рассмотрим осадку штампа (см. схему) и сопоставим действительную картину деформирования основания, полученную экспериментально, с расчётами по теории Фусса-Винклера (теория местных упругих деформаций) и упругого полупространства.
Схема деформирования основания за пределами загруженной площади (эксперимент и теории). Как видно из представленного рисунка, действительная картина деформации грунта за пределами загруженной поверхности, расположена между результатами расчета по гипотезе упругого полупространства и гипотезе Фусса-Винклера. Решение по теории местных упругих деформаций. Как уже отмечалось ранее, по данному методу установлена прямая зависимость между контактными напряжениями по подошвы фундамента (балки) Px и деформациями Zx:
где Px [кг/см2] – интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х); Zx [см] – величина перемещения в т. Х (зависит от жесткости балок, характера распределения нагрузки, размеров балки и деформируемости основания); Сz [кг/см3] – коэффициент постели (упругости основания). Основные обозначения для решения задач по данному методу приведены на схеме.
Расчётная схема к решению задачи деформации балки на упругом основании по методу местных упругих деформаций. Впервые этот метод был применён при расчете шпал под железную дорогу, тогда считали, что Сz = f (грунта), но потом выяснилось, что Сz = f (грунта и ширины подошвы фундамента).
Вычислив Zx и используя коэффициент постели Сz, находим Рх, а затем величину момента Мх и поперечных сил Qx в различных сечениях фундамента – балки: Решение этой задачи во многих случаях приведено в табличной форме в зависимости от конструкции фундаментов (см. справочник проектировщика). Решение по методу упругого полупространства. В этом случае также используется дифференциальное уравнение изогнутой оси балки, но прогиб балки определяется с использованием выражений как для упругого полупространства. При этом упругое полупространство заменяется линейно-деформируемым полупространством, деформационные свойства которого характеризуются модулем общей деформации и коэффициентом Пуассона. для случая плоской деформации - решение Фламана
для случая пространственной и осесимметричной деформации - решение Буссинеска
Решения уравнения для линейно-деформируемого полупространства приводятся у Б.Н.Жемочкина, М.И.Горбунова-Посадова и др. Имеются детальные таблицы [13]. Решая дифференциальное уравнение изогнутой оси балки для ленточных фундаментов и для плитных фундаментов, находят реактивное давление грунта под подошвой фундаментов, а по нему изгибающие моменты и поперечные силы. После этого по известным значениям M и Q уточняется сечение фундамента и проектируется его армирование.
40. Предельное напряжение состояний массива грунта. Фазы работы грунтового основания. Предельное напряженное состоянием массива грунта, такое при котором малейшее добавочное силовое воздействие или малейшее уменьшение прочности грунта может привести к нарушению существующего равновесия – к потере устойчивости массива: возникновению в нем поверхности скольжения, развитию различных сдвиговых деформаций и нарушению природной структуры. Обычно нарушение равновесия приводит к выпору грунта из под фундамента, что сопровождается большой осадкой. Т.к. это не допустимо для большинства сооружений важно правильно определить максимальную возможную нагрузку на грунтовое основание. Различают 3 фазы работы грунтового основания:
1 фаза. Осадки пропорциональны давлению сдвиговых деформаций в массиве. Эта фаза ограничивается Рнк (рассматривается по 2 группе предельных состояний по деформациям) 2 фаза. Фаза сдвигов – в массиве в отдельных точках появляются сдвиговые (пластические) деформации, которые с увеличением нагрузки растут а в конце фазы определяемом конечным критическим давлением – Ркк сдвиговые деформации сливаются, образуя поверхности скольжения в этот момент начинается потеря устойчивости всего массива. 3 фаза. Фаза сплошных сдвигов – характеризуется наличием сплошных поверхностей скольжения – полная потеря устойчивости основания (расчет по 1 группе предельных состояний на прочность занимается определением Ркк для данного массива).
41. Определение начального критического давления. Условия равновесия внутри массива под нагрзкой. Sinφ=(σ1-σ3)/(σ1+σ3+2C*ctgφ) Массив в линейно деформируемом полупространством можем написать выражения для главных напряжений в любой точке любого сечения массива при известной нагрузке на поверхности. Решение теории упругости при полосовой нагрузке σ1=Р(α+sinα)/π; σ2=Р(α-sinα)/π
42. Определение конечного критического давления.
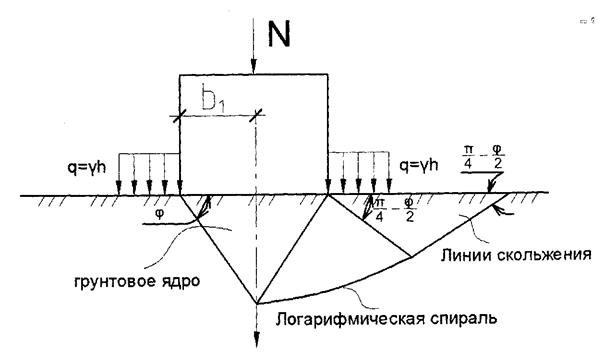
При работе фундамента во II и III фазах возможно опрокидывание фундамента из-за появления сплошных поверхностей скольжения. При этом будет происходить сдвиг слоев грунта по плоскостям скольжения и выпор грунта на поверхность:
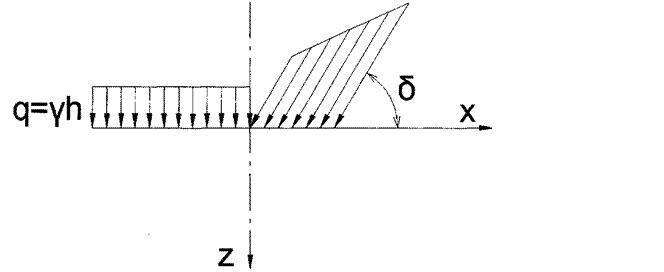
На основании опытных данных К.Терцаги предложил схему деформируемого грунта и на ее основе получил формулу: Рк.к. = Nγγh+ Nqq+ Ncc Где, Nγ;Nq;Nc - коэффициенты, зависящие от φ и определяются по таблицам; b1 - полуширина фундамента; q= γН - боковая пригрузка; С -удельное сцепление. Наиболее полное решение получено в 1952 году В.В.Соколовским для случая плоской задачи при. действии на поверхности нагрузки, наклоненной под углом б к вертикали, изменяющейся по закону трапеции:
Рк.к = Аγх + Bq+ Сс где, А, В, С - коэффициенты зависящие от φ и
43. Расчет конечных осадок
Различают два вида осадок: 1. Конечная осадка - осадка, рассчитываемая на основе модели линейно-деформируемого полупространства, когда все давление воспринимается скелетом грунта. 2. Осадка во времени - осадка, рассчитываемая на основе теории фильтрационной консолидации (уплотнения)
Расчет конечных осадок.
Существует выражения для определения относительной вертикальной деформации при трехосном напряженном состоянии (теория упругости):
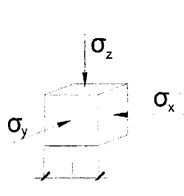
Единичный обьем:
Деформации единичного объема: εz=[σz-μ(σx-σy)]/E Для вычисления осадки полупространства необходимо проинтегрировать последнее выражение S=(Интеграл от 0 до ∞) εz dz
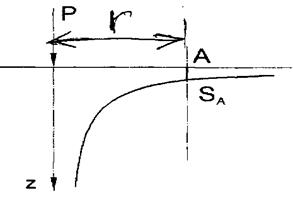
В случае сосредоточенной силы, приложенной к полупространству:
SA=P(1-μ2)/πEr
где, Р - сосредоточенная сила; Е - модуль деформации; μ- коэффициент Пуассона; r – расстояние от точки А до места приложения нагрузки В случае равномерно распределенной нагрузки пользуются методом перехода к элементарным сосредоточенным силам и интегрированию по всех площади загружения. В результате получают формулу для определения осадки полупространства:
S=qbω(1-μ2)/E где, q - распределенная нагрузка; ω- коэффициент, зависящий от формы загруженной площади и местоположения точки.
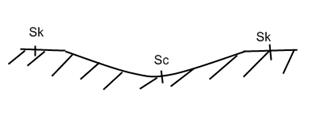
Это решение получено при условии, что нагрузка гибкая:
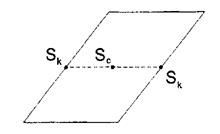
Можно показать, что средняя осадка гибкого фундамента: Scp=(2Sk+Sc)/3 Эта величина близка к величине осадки абсолютно жесткого штампа, поэтому решения упрощается и коэффициент ω будет зависеть только от формы загруженной площади - формы штампа (фундамента)
Для жесткого штампа наше решение принимает вид формулы Шлейхера:
E0=ω(1-μ02)Pb/S S=Pbω(1-μ02)/E0
p- давление на подошву фундамента b- диаметр или сторона фундамента; E0-модуль деформации грунта; Этой формулой можно пользоваться для определения осадки основания фундамента в ограниченных случаях.
В СНиПе предусмотрен другой метод расчета осадок оснований. Он основан на схеме работы грунта при невозможности бокового расширения. Это дает возможность выразить напряжения по осям X и Y через σz σx=σy=μσz/(1-μ) Тогда выражение для вычисления деформаций единичного обьема грунта основания примет вид:
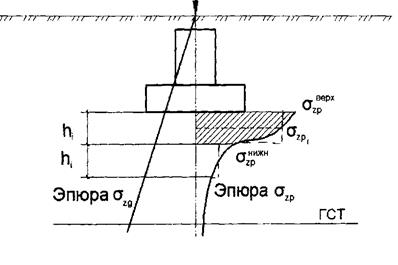
εz=(1-[2μ0/(1-μ0)])σz/E0 где β=(1-2μ02)/(1-μ0)=0,8 согласно СНиП для всех грунтов Задача расчета осадки основания сводиться к вычислению интеграла. СНиП предусматривает вычисление интеграла численным методом путем разбиения грунтовой толщи основания на отдельные элементарные слои толциной hi и при этом вводятся следующие допущения: 1. Каждый элементарный слой имеет постоянные Е0 и μ0 2. Напряжение в элементарном слое постоянно по глубине и равно полусумме верхнего и нижнего напряжений 3. Имеется граница сжмаемой толщи на глубине, где σzp=0.2σzq (где σzq напряжение от собственного веса грунта)
44. Алгоритм расчета осадки основания фундамента 1. Основание разбивается на элементарные слои толщиной; где hi<0.4b, b- ширина подошвы фундамента. 2. Строиться эпюра нарпяжений от собственного веса грунта σzq 3. Строиться эпюра напряжений от внешней нагрузки σzp 4. Устанавливается граница сжимаемой толщи. 5. Определяетсяя напряжение в каждом элементарном слое:
σzpi=(σzpверх +σzpниж)/2
6. Рассчитывается осадка каждого элементарного слоя: Si=βσzpihi/Ei
7. Вычисляется конечная осадка основания фундамента, как сумма осадок
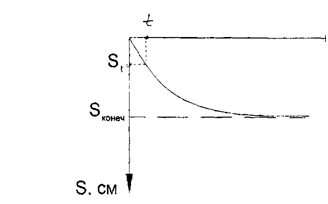
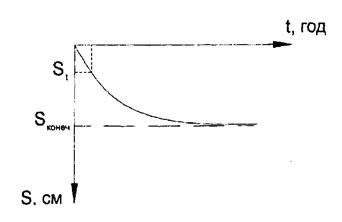
При наблюдении за осадками оснований фундаментов был получен график развития осадок во времени.
Вводиться понятие степени консолидации: U=St/SKOH
Конечная осадка рассчитывается методом СНиП. Степень консолидации определяется решением дифференциального уравнения одномерной фильтрации: U=1-16(1-2/π)e-N/π2+(1+2/(3π))e-9N/9+… Физический смысл степени консолидации выражает величина показателя N: N=π2kФt/(4m0h2γω)
Где, kФ ~ коэффициент фильтрации, [см/год] m0 – коэффициент относительной сжимаемости слоя; [см2/кг] h - толщина сжимаемого слоя; [см] t - время; [год] γω - удельный вес воды
Пример Определить осадку основания фундамента через 1, 2 года и 5 лет. Давление под подошвой фундамента р = 2 кгс/см2; грунт - суглинок; толщина сжимаемого слоя 5м; коэффициент фильтрации kФ = 10 -8 см/сек; Коэффициент относительной сжимаемости суглинка m0=0,01 см2/кг. 1. Определяем величину коэффициента консолидации: ^Пе ревод из секунд в год СV=kФ/(m0γω)=(10-8*3*107){см/год}/(0.01{см2/кг}*0,001)=3*104 см2/год 2. Определяем величину N: N= π2 СVt/(4h2)=0.3t
3. Определяем величину степени консолидации: U1=1-16(1-2/π)e-0.3t/π2 U1=0.39 U2=0.55 U3=0.82 4. Вычисляем величину конечной осадки: S=hm0p=500*0.01*2=10 см 5. Вычисляем осадки во времени, как:
|

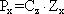 ,
,
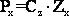 ,
,

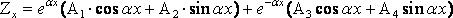
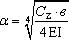
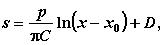


 45. Понятие о расчете осадок во времени
45. Понятие о расчете осадок во времени



