Теорема про перетворення інтеграла
Теорема лінійності Перетворення лінійної комбінації (суми) функцій дорівнює сумі перетворень (зображень) цих функцій: L [ f 1(t) + a 2 f 2(t) + …] = a 1 Lf 1(t) + a 2 Lf 2(t) + … = a 1 F 1(s) + a 2 F 2(s) + … (1.9) Теорема перетворення похідної L [ f ' (t)] = sL[ f (t)] – f (0) = s F (s) – f (0), (1.10) f (0) – початкові умови, або значення функції f (t) для t = 0. Для нульових початкових умов перетворення Лапласа для похідних n-го порядку обчислюється за формулою L [ f n(t)] = sn F (s). (1.11) Теорема про перетворення інтеграла
Отже, операція диференціювання в перетворенні Лапласа відповідає множенню зображення на оператор s, а операція інтегрування – діленню зображення на оператор s. Тому виконання операцій диференціювання та інтегрування зображень значно спрощується.
|
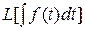= L[ f (t)]/s = F (s)/s. (1.12)
