Верховой откос
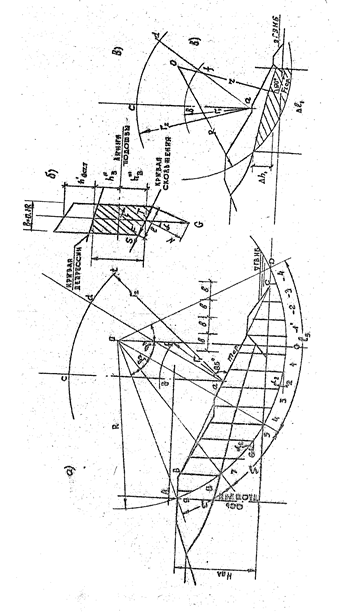
1. Первый расчетный случай (основной) – принимается максимально возможное снижение уровня воды в водохранилище от НПУ с наибольшей возможной скоростью; при этом учитываются фильтрационные силы, возникающие в откосе. 2. Второй расчетный случай (особый) – уровень воды в верхнем бьефе находится на самой низкой отметке, но не ниже 0,2 Нd, где Нd – расстояние от гребня плотины до дна в верхнем бьефе; уровень грунтовой воды в теле плотины принимается на той же отметке, что и уровень воды в водохранилище. 3. Третий расчетный случай (особый) – принимается максимально возможное снижение уровня воды в верхнем бьефе с наибольшей возможной скоростью, начавшееся от ФПУ; при этом учитываются фильтрационные силы, возникающие в откосе. Устойчивость откосов плотин должна быть обеспечена при всех возможных условиях эксплуатации, а такие в процессе возведения плотины. Расчет устойчивости откосов плотин из грунтовых материалов методом Терцаги. При выполнении расчетов устойчивости откоса земляной плотины методом Терцаги намечают некоторую круглцилиндрическую поверхность обрушения радиусом R, проведенную из центра О (рис. 2.30). Кривая обрушения и внешний контур плотины ограничивают область обрушения.
Рис. 2.30. Схема к расчету устойчивости низового откоса земляной плотины Определение коэффициента устойчивости откоса для этой области обрушения производится в такой последовательности. 1. Расчетная область обрушения разбивается вертикальными линиями на фрагменты с номерами i (рис. 2.30 а). Для удобства вычислений ширина каждого фрагмента b принимается равной b = 0.1 · R. При этом середина нулевого фрагмента принимается на вертикали, проходящей через центр О. Крайние фрагменты могут иметь ширину bi меньшую, чем b = 0.1 · R. 2. Определяются значения синусов sin a и косинусов cos a углов наклона подошвы каждого из фрагментов к горизонту a. При принятой ширине фрагментов b = 0.1 · R очевидно значения sin ai могут быть приняты следующим образом: sin a 0 = 0, sin a 1 = 0.1, sin a 2 = 0.2 и т.д. Для крайних фрагментов значения sin a i определяются как соответствующие отношения расстояния по горизонтали от середины подошвы крайнего фрагмента до вертикали, которая проходит через центр О. Значения cos ai могут быть найдены по формуле
3. Определяются значения веса каждого фрагмента Gi. Для этого по чертежу (схеме) графически находятся средние значения высоты слоя грунта тела плотины естественной влажности h´ ест, высоты слоя насыщенного водой грунта тела плотины h´´н, высоты слоя насыщенного водой грунта основания h´´´н. После этого вычисляются значения Gi по формуле Gi = [ r ´ ес т · g · h´ ест + (r ´´ н – rw) · g · h´´н + (r´´´н – rw) · g · h´´´н ] · bi, (2.22) где r ´ ес т – плотность грунта тела плотины естественной влажности; r ´´ н – плотность насыщенного водой грунта тела плотины; r´´´н – плотность насыщенного водой грунта основания; rw – плотность воды; g – ускорение свободного падения; bi – ширина фрагмента. 4. Для каждого фрагмента находятся значения величины Gi · sin ai. 5. Определяются значения длины подошвы каждого из фрагментов li по формуле
6. Определяются значения тангенса угла внутреннего трения tg ji и удельного сцепления сi в пределах подошвы каждого фрагмента в зависимости от грунта, в котором располагается эта подошва (грунт тела плотины естественной влажности, насыщенный водой грунт тела плотины, насыщенный водой грунт тела основания). В случае если подошва i -го фрагмента расположена в двух грунтах с характеристиками соответственно tg j 1, с 1 и tg j 2, с 2 необходимо поступить следующим образом. Сначала определить длины участков подошвы фрагмента, соответствующих 1-му грунту l 1 i и 2-му 1-му грунту l 2 i. После этого вычисляются расчетные значения tg ji и удельного сцепления сi по формулам
7. Находятся значения величины Gi · cos aI · tg ji. 8. Вычисляются значения произведений сi · li. 9. Определяется площадь насыщенной водой части области обрушения А, в пределах которой следует учитывать гидродинамические силы, вызываемые фильтрационным потоком. Эта часть области обрушения ограничена сверху кривой депрессии, снизу – кривой обрушения, а справа – вертикалью, которая проходит через точку входа кривой депрессии в дренаж (рис. 2. 30 в). Одновременно определяются координаты центра тяжести площади насыщенной водой части области обрушения, в пределах которой следует учитывать гидродинамические силы. Кроме того, определяется значение радиуса r, соответствующего положению центра тяжести площади насыщенной водой части области обрушения. 10. Находится значение среднего уклона кривой депрессии i в пределах насыщенной водой части области обрушения до вертикали, которая проходит через точку входа кривой депрессии в дренаж. Значение i определяется как отношение i = Δ h 1 / Δ l 1. величины Δ h 1 и Δ l показаны на рис. 2. 30 в. 11. Определяется значение коэффициента устойчивости откоса плотины ks по формуле
Последовательность расчета устойчивости низового откоса земляной плотины дана в приведенном ниже примере 2.11. Определение размеров и положения области опасных центров кривых обрушения. Как уже указывалось выше, при выполнении расчетов устойчивости откосов плотин рассматривается несколько возможных круглоцилиндрических поверхностей (кривых) обрушения. Область опасных центров кривых обрушения может быть найдена следующим образом (рис. 2.30 в). Из середины откоса (или осредненного откоса) (точка а на рис. 2.30 в) проводятся вертикальный луч ас и луч аd под углом 85 к откосу (или осредненному откосу) ad. Далее из точки а проводят дуги радиусами r 1 и r 2. Полученная таким образом область bcdf является областью опасных центров кривых обрушения. Значения радиусов r 1 и r 2 могут быть приняты в соответствии с табл. 2.6 в зависимости от высоты плотины Hd и коэффициента заложения откоса (или осредненного откоса) m. Для промежуточных значений m радиусы r 1 и r 2 определяются по линейной интерполяции.
К определению радиусов r 1 и r 2 Таблица 2.6
В курсовом проекте в пределах области bcdf выбирается центр кривой обрушения О и принимается радиус этой кривой R таким образом, чтобы кривая обрушения захватывала примерно половину гребня плотины и часть основания. В случае скального основания кривая обрушения должна лишь касаться скального основания. Пример 2.11. Расчет устойчивости низового откоса плотины
|

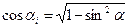 . (2.21)
. (2.21)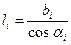 . (2.23)
. (2.23)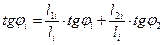 ,
, 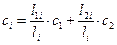 . (2.24)
. (2.24)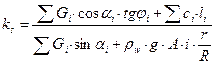 . (2.25)
. (2.25)


