Точечная и интервальная оценка среднего значения признака в генеральной совокупности по данным большой выборки
Условие:имеются данные выборочного наблюдения о годовой заработной плате работников, занятых в сельском хозяйстве (таблица 2.1.) Численность выборки составляет n=36. Провести точечную и интервальную оценку среднего значения признака генеральной совокупности (среднего значения заработной платы 90 тысяч работников в районе).
Таблица -2.1 Годовая заработная плата работников, занятых в сельском хозяйстве по данным выборочного наблюдения
Решение: 1. Определим квадраты значений признака (хi2) и запишем их в таблицу 2.1. 2. Подсчитаем 3. Вычислим среднюю величину по данным выборочной совокупности:
4. Найдем выборочную дисперсию:
5. Исчислим несмещенную оценку[1] дисперсии:
Несмещенная оценка дисперсии может быть исчислена также без определения выборочной дисперсии по формуле
6. Рассчитаем среднюю ошибку выборочной средней:
Примечание: так как число выборки по отношению к числу единиц генеральной совокупности чрезвычайно мало, то поправочным коэффициентом 7. Проведем точечную оценку средней в генеральной совокупности:
8. По таблице "Значение интеграла вероятностей при разных значениях t" (приложение 1) найдем теоретическое значение t при доверительном уровне вероятности 9. Определим предельную случайную ошибку выборочной средней:
10. Проведем интервальную оценку, т.е. найдем интервал, в котором с заданным уровнем вероятности находится средняя генеральной совокупности:
11. Сделаем вывод. С доверительным уровнем вероятности 0,95 можно утверждать, что среднегодовая заработная плата 1 работника в районе находится в пределах от 249,38 до 252,62 тыс.руб.
|

 и
и  и также запишем в таблицу 2.1.
и также запишем в таблицу 2.1.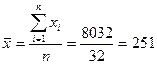 (тыс.руб.)
(тыс.руб.)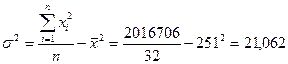
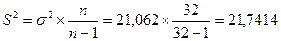

 (тыс.руб.)
(тыс.руб.) можно пренебречь.
можно пренебречь. (тыс.руб.) при m x = 0,82 тыс.руб
(тыс.руб.) при m x = 0,82 тыс.руб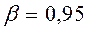 : t 0,95=1,96.
: t 0,95=1,96.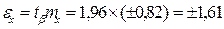 9 (тыс.руб.)
9 (тыс.руб.)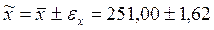 или
или 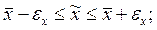
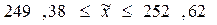 (тыс.руб.)
(тыс.руб.)


