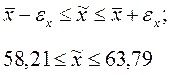Точечная и интервальная оценка средней величины генеральной совокупности по данным малой выборки
Условие: Имеются данные выборочного наблюдения о массе плодов (яблок) из партии продукции 1 тонна (таблица 2.2) Провести точечную и интервальную оценку средней генеральной совокупности. Таблица -2.2 Масса плодов по данным выборочного наблюдения, граммов
Решение: 1.Определим квадраты значений признака (Х i) и запишем их в таблицу 2.2 2. Подсчитаем суммы 3. Вычислим среднюю величину массы плодов по данным выборочной совокупности:
4.Найдем выборочную дисперсию:
5. Исчислим несмещенную оценку дисперсии:
6. Исчислим среднюю ошибку выборочной средней:
Примечание: так как число выборки по отношению к числу единиц генеральной совокупности чрезвычайно мало, то поправочным коэффициентом 7. Проведем точечную оценку средней в генеральной совокупности:
8. По таблице "Значения двухстороннего критерия t-Стьюдента (приложение 2) найдем теоретическое значение t при доверительном уровне вероятности 9. Определим предельную случайную ошибку выборочной средней:
10. Проведем интервальную оценку средней в генеральной совокупности:
Сделаем вывод. С доверительным уровнем вероятности 0,95 можно утверждать, что средняя в генеральной совокупности находится в пределах от 58,21 до 63,79 г.
[1] Несмещенную оценку дисперсии необходимо рассчитывать, прежде всего, для совокупностей менее 30 единиц
|

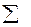 Х i и
Х i и 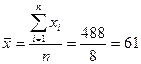 (г)
(г)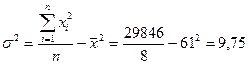
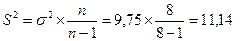
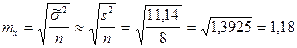 (г)
(г) можно пренебречь.
можно пренебречь.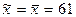 (г) при m x = 1,18 (г)
(г) при m x = 1,18 (г)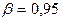 и числе степеней свободы вариации
и числе степеней свободы вариации  = п -1 = 7: t0,95=2,3646.
= п -1 = 7: t0,95=2,3646.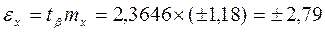 (г)
(г)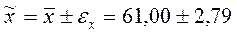 (г) или
(г) или