В. И. Диденко, А. В. Иванов
681.142.681 Метрологический подход к исследованию шума квантования дельта-сигма АЦП В. И. Диденко, А. В. Иванов Московский энергетический институт (технический университет), Москва, Россия, e-mail: didenkovi@mail.ru
Предложен метрологический подход к анализу шумов квантования дельта-сигма АЦП. Определены отличия истинных сигналов на выходе модулятора от идеальных. Найдены зависимости шума квантования от амплитуды входного сигнала и полосы частот. Ключевые слова: дельта-сигма АЦП, шум квантования.
The metrological approach to analysis of quantization noise is proposed. The differences between true signals and ideal ones at modulator output are defined. The dependences of the quantization noise from input signal and frequency band is found. Key words: delta-sigma ADC, quantization noise.
Любой аналого-цифровой преобразователь (АЦП) характеризуется квантом q. Погрешность квантования является систематической, зависит от входного сигнала и лежит в пределах ± 0,5 q. Если входной сигнал предполагается случайным, то при определенных допущениях погрешность квантования становится случайной величиной с равномерным законом распределения. Ее среднее квадратическое отклонение (СКО) можно найти по формуле:
В большинстве АЦП уменьшение СКОсвязано с пропорциональным аппаратурным усложнением, например, увеличением числа компараторов, повышением разрядности цифроаналогого преобразователя (ЦАП) и т. д. Другим направлением по снижению СКО является применение так называемых стохастических АЦП [1]. Суть этого направления состоит в квантовании суммы преобразуемого и опорного случайного сигналов. В результате на выходе даже при постоянном входном сигнале код имеет несколько значений, вероятность появления которых зависит от преобразуемого сигнала. После цифровой фильтрации СКО результата можно получить существенно меньше, вычисленного по (1). Благодаря ряду достоинств, все более широкое распространение находят дельта-сигма аналого-цифровые преобразователи (ДСАЦП) [2 – 4]. По существу, этот тип АЦП можно рассматривать как разновидность стохастического преобразователя. Его особенностями являются, во-первых, естественное включение источника шума в структуру АЦП, а во-вторых, простота смещения спектра шума в область высоких частот. При уменьшении верхней частоты пропускания цифрового фильтра весьма эффективно снижается СКО шума. Для модулятора первого порядка СКО шума квантования в функции указанной частоты растет с наклоном 30 дБ/дек (9 дБ/окт), для модулятора второго порядка с наклоном 50 дБ/дек (15 дБ/окт) и т. д. [5 – 7]. Шум квантования ДСАЦП исследовали, в основном, с помощью имитационного моделирования. Аналитическое моделирование шума вели в предположении, что он имеет тот же характер, что и погрешность квантования, рассмотренная выше [5, 6]. Однако такой подход не имеет строгого научного обоснования [5] и плохо согласуется с практикой [8]. Тем не менее, более адекватной теории не было предложено. Такую попытку делают авторы. Модель ДСАЦП с модулятором первого порядка. Обычно ДСАЦП состоит из последовательно соединенных дельта-сигма модулятора (далее модулятора) и цифрового фильтра [1, 3]. В простейшем случае модулятор (малоразрядный АЦП) представляет собой структуру с астатической обратной связью (рис. 1). В его прямой цепи включен интегратор и компаратор-защелка (однобитовый квантователь), работой которого управляет стробирующий сигнал с частотой выборки f в. В цепи обратной связи находится однобитный ЦАП (± V оп – опорные напряжения), разность его входного и выходного сигналов поступает на интегратор. Из приведенной структуры, в частности, видно происхождение названия рассматриваемого класса АЦП. Вычитание двух сигналов соответствует символу Δ, а интегрирование – символу Σ. В некоторых публикациях эти символы меняют местами, что не имеет никакого значения.
Рис. 1. ДСАЦП с модулятором первого порядка: 1 – сумматор; 2 – интегратор; 3 – компаратор-защелка; 4 – цифровой фильтр и дециматор; 5 – 1-битный ЦАП
Пусть входное напряжение V вх постоянного тока лежит в пределах ± V оп. Введем в рассмотрение нормированный сигнал X на входе модулятора, полученный делением реального сигнала V вх на V оп. Очевидно, –1 ≤ X ≤ 1. Сигнал Y на выходе модулятора является логическим и имеет только два уровня, соответствующих –1 и +1 в единицах входного сигнала. Основой предложенного метрологического подхода к анализу шумов квантования служит представление модулятора ДСАЦП измерительным преобразователем с идеальным коэффициентом передачи, равным единице. Тогда отличия истинных сигналов на выходе модулятора от идеальных представляют шум квантования модулятора, если его узлы идеальны. Номинальная (идеальная) функция преобразования модулятора описывается функцией Y = X, а его погрешностью будет отклонение Y от X. Абсолютная погрешность модулятора в каждый момент времени (по входу или по выходу) определяется как Δ = Y – X. На выходе модулятора возможны только два значения погрешности: Δ1 = –1– X при Y = –1 и Δ2 = 1– X при Y = +1. Вероятности их появления (соответственно P 1 и P 2) зависят от входного сигнала и отличия характеристик отдельных узлов модулятора от идеальных. Назовем шумом квантования модулятора изменение его погрешности во времени при идеальных узлах. Найдем характеристики этого шума. Для постоянного входного сигнала и достаточно большого интервала наблюдения частóты появления -1 и +1 стремятся соответственно к P 1 и P 2, причем P 1 + P 2 = 1, а среднее нормированное напряжение на выходе ЦАП составляет P 2 – P 1. При идеальных узлах модулятора его входное напряжение будет P 2 – P 1 = X. Решая полученную систему из двух уравнений, находим P 1 = 0,5(1– X) и P 2 = 0,5(1+ X). Таким образом, шум квантования при постоянном входном сигнале описывается законом дискретного двузначного распределения. Его математическое ожидание:
и дисперсия:
Выражения (2) и (3) справедливы для модулятора любого порядка с однобитовым квантователем. В отличие от классического подхода [5 – 7] в выражении (3) присутствует зависимость от входного сигнала. Значение СКО шума становится равным нулю на концах диапазона (X = ±1) и достигает единицы в его середине (X = 0). Выражение (3) справедливо для всего диапазона частот шума квантования от 0 до f в/2 и представляется абсолютно точным для принятой структуры модулятора. Верхний предел диапазона частот определяется тем, что при максимально быстром изменении сигнала +1; –1; +1; –1 и т. д. период повторения равен двум периодам частоты выборки. На практике основной интерес представляет шум квантования в узкой низкочастотной полосе (полосе пропускания цифрового фильтра). Для нахождения такого шума модулятор изображают линейной моделью (рис. 2) [5], в которой нелинейный элемент – компаратор заменен линейным усилителем с некоторым эквивалентным коэффициентом усиления η и аддитивным источником шума квантования ε с равномерной спектральной плотностью мощности шума компаратора S ε.
Рис. 2. Функциональная схема модулятора с линейной моделью компаратора
Для линеаризованной модели спектральную плотность мощности шума квантования Δ на выходе модулятора можно определить по формуле [9]:
где τ – постоянная времени интегратора. Для дисперсии шума квантования в полосе частот от нуля до любого f ≤ f в/2 справедливо выражение [9]:
При f = f в/2 выражение (4) должно сводиться к (3), откуда:
Подставив (5) в (4), получим:
При полосе частот от 0 до f << 0,5 f в (6) можно упростить:
В [5 – 7] эквивалентный коэффициент усиления компаратора принимали как η = τ f в без какого-либо обоснования. Рассмотрим, правомерно ли это. Поставим условие, что задержка реального модулятора на низких частотах должна быть такой же, как у линейной модели. В общем случае модулятор имеет задержку от 0 до 1/ f в, так как стробирующий сигнал может придти на бесконечно малый интервал времени раньше или позже изменения полярности на входе компаратора. В среднем задержка составит 1/2 f в. Для получения такой задержки на низкой частоте эквивалентный коэффициент усиления должен быть η = 2τ f в. Действительно, при этом задержка модулятора по времени в области сравнительно низких частот примерно равна 1/2 f в, а (7) преобразуется соответственно к виду:
где RF = f в/2 f – отношение всей полосы частот шума на выходе модулятора к полосе частот, в которой определяется шум квантования. До сих пор анализ проводился для постоянного сигнала. Между тем, в настоящее время шумы и другие параметры АЦП принято исследовать и нормировать при переменном входном сигнале, чаще всего – синусоидальном. Если на вход модулятора подать синусоидальный сигнал амплитудой a, то дисперсия шума квантования на выходе модулятора во всей частотной полосе будет [9]:
Распределение шума по частотам для синусоидального входного сигнала имеет зависимость, схожую с (6):
На низких частотах отношение сигнал–шум для η = 2τ f в можно округленно представить как:
В теории [5 – 7], построенной на базе (1), при η = τ f в для модулятора первого порядка используется выражение:
где R – коэффициент деления частоты на выходе цифрового фильтра (см. рис. 1). На примере сравнения выражений (8) и (9) рассмотрим различия использования известной [5 – 7] и предложенной теорий. Для этой цели приведем (9) к виду:
Качественное отличие (8) от (10) состоит в том, что выявлена зависимость шума квантования от амплитуды входного сигнала. В [5 – 7] предполагается, что эта зависимость отсутствует, тогда отношение сигнала к шуму оказывается пропорциональным амплитуде синусоидального сигнала. При новом подходе для постоянного входного сигнала, согласно (3) СКО шума стремится к нулю, когда | Х |→1, и принимает максимальное значение 1, когда X = 0. Для синусоидального входного сигнала уменьшение шума с увеличением входного сигнала имеется, но не столь существенное (в Числовой множитель в (10) больше, чем в (8). Коэффициенты RF в (8) и R в (9) или (10) совпадают, если только частота сигнала на выходе цифрового фильтра в два раза превышает его полосу пропускания. В реальных фильтрах это соотношение может не выполняться. На выходе цифрового фильтра можно получить шаг квантования меньше СКО шума квантования. На практике вводится округление до кванта q, значение которого больше СКО. При этом, как и в любом АЦП, возникает погрешность квантования, описанная в начале статьи. Результаты моделирования. Для проверки полученных аналитических выражений были использованы прикладной пакет программ Matlab 6.5 с Simulink 5 и стандартная схема ДСАЦП с модулятором первого порядка. Частота выборки входного сигнала f в =512∙1024 Гц. Будем рассматривать только положительный входной поддиапазон, так как функция СКО является четной. Для проверки фундаментального выражения (3) на вход модулятора подавали множество постоянных сигналов { X }, состоящее из n значений. Каждое значение Xi случайно выбиралось на интервале [0; 1] по закону равномерной плотности. Для каждого Xi снимали последовательность из N отсчетов с выхода модулятора и по ним вычисляли СКО. Расхождение между результатами моделирования и аналитическим выражением (3) лежит в ожидаемых для заданного числа отсчетов пределах [9]. Например, для X = 0,97 и N = 14000 расхождение составляет всего 0,22 %. Выражение (3) также было проверено другим методом. Для различных Xi строили амплитудный спектр, используя быстрое преобразование Фурье (БПФ) с числом точек N = 8192 для каждого Xi. Оценку СКО для Xi вычисляли по формуле:
где Umj – амплитуда j -й гармоники в спектре. Моделирование показало, что максимальное различие между (3) и (11) достигается в точке Х = 0,86 и составляет 4,3 %. При увеличении числа точек БПФ это различие уменьшается с наклоном примерно –20 дБ/дек и при N = 32768 уже не превышает 0,4 % в той же точке. Описанное выше моделирование соответствует всей полосе частот (от 0 до f в/2). Как и следовало ожидать, аналитическое моделирование в данном случае оказалось абсолютно точным, а имитационное моделирование может только приближаться к нему при неограниченном увеличении объема выборки. Насколько известно, ранее имитационное моделирование всегда считалось эталонным по отношению к аналитическому при исследовании ДСАЦП.
Рис. 3. Сравнение теоретической зависимости СКО от полосы частот по формуле (6) с результатами моделирования для некоторых постоянных входных сигналов Xi и с усредненным СКО
Чтобы проверить (6), необходимо получить Как следует из рис. 3, для отдельных Xi расхождения между результатами моделирования и зависимостью (6) могут быть большими, что указывает на ограниченное применение допущения о равномерном спектре шума компаратора. Однако, если провести усреднение
то для равномерно распределенных Xi в диапазоне [0; 1] полученный результат будет близок к зависимости (6) (см. кривую Среднее относительное отклонение δcp вычисляли во всех N /2 точках шкалы частот по формуле:
где
Выше было предложено выбрать эквивалентный коэффициент усиления η; равным 2 τfS. Теперь при моделировании найдём опытным путём этот коэффициент из условия, что он должен дать наименьшее значение корня из суммы квадратов отклонений:
Из таблицы следует, что при увеличении числа точек усреднения полученный опытным путем эквивалентный коэффициент усиления приближается к h = 2τ f в (а не к τ f в, как было принято в [5 – 7]). Так же уменьшаются значения dср и dS. Для определения временной задержки модулятора на его вход подавали синусоидальные сигналы с частотами 100 Гц, 1 и 10 кГц и оценивали фазовый сдвиг первой гармоники при помощи БПФ. Полученные временные сдвиги отличаются от теоретического значения 1/2 f в меньше чем на 2·10-8. Выводы. Применение метрологического подхода к исследованию шума квантования ДСАЦП позволило: определить погрешности дельта-сигма модулятора и выявить, что для постоянного входного сигнала погрешность шума квантования модулятора имеет дискретный двузначный закон распределения; подтвердить, что СКО этого закона зависит от входного сигнала в соответствии с (3), причем при увеличении числа точек расхождение между результатами моделирования и (3) может быть сведено к сколь угодно малой величине; найти аналитическую зависимость СКО шума квантования от полосы частот, в которой оно вычисляется. Эта зависимость хорошо сочетается с результатами моделирования только при их усреднении; выбрать эквивалентный коэффициент усиления компаратора и определить фазовую задержку модулятора, которые подтверждаются результатами моделирования. Анализ проведен для простейшего ДСАЦП, но многие его результаты могут быть использованы и для более сложных схем. Литература 1. Виксна А. Ж., Прокофьев Ю. П., Смильгис Р. Л. // Приборы и техника эксперимента. – 1981. – № 6. – С. 20. 2. Carnì D. L., Grimaldi D. //Proc. 12 th TC4 Intern. Workshop ADC Modelling and Testing. – Iaşi (Rumania), 2007. – P. 91. 3. Mariano A., Dallet D., Deval Y., Bégueret J-B. //Ibid. – P. 118. 4. Шахов Э. К. //Датчики и системы. – 2006. – № 12. – С. 50. 5. Benabes P., Aldebert P., Kielbasa R. //Proc. Intern. Workshop ADC Modelling and Тesting. – Bordeaux (France), 1999. – P. 3. 6. System application guide. – Analog Devices (USA), 1993. – P. 14.1. 7. Application Note 1870 “Demystifying Sigma-Delta ADCs”, 2005. 8. Davis A. J., Fisher G. //Computer Standards & Interfaces. – 1998. – V. 19. – P. 189. 9. Didenko V. I., Ivanov A. V., Teplovodskiy A. V. //Proc. 12 th TC4 Intern. Workshop ADC Modelling and Testing. – Iaşi (Rumania), 2007. – P. 3.
Дата принятия 29.01.2009 г.
|

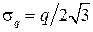 . (1)
. (1)
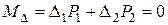 (2)
(2) . (3)
. (3)
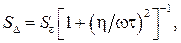
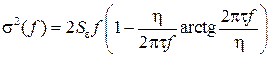 . (4)
. (4) . (5)
. (5)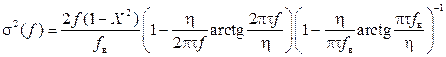 . (6)
. (6)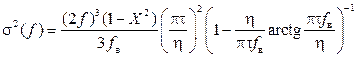 . (7)
. (7)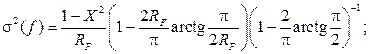
 ,
, .
. .
. . (8)
. (8)
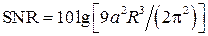 , (9)
, (9)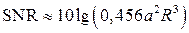 . (10)
. (10)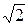 раз, когда амплитуда синусоидального сигнала меняется от 0 до 1).
раз, когда амплитуда синусоидального сигнала меняется от 0 до 1). , (11)
, (11)
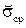 . Все зависимости нормированы (разделены на 1 – Х 2)
. Все зависимости нормированы (разделены на 1 – Х 2) (f) – зависимость
(f) – зависимость 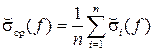 , (12)
, (12) (f) на рис. 3). Результаты такого моделирования приведены в таблице как функция от числа точек n, по которым проводится усреднение. На рис. 3 зависимости построены для n = 500.
(f) на рис. 3). Результаты такого моделирования приведены в таблице как функция от числа точек n, по которым проводится усреднение. На рис. 3 зависимости построены для n = 500.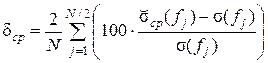 , %,
, %, – значение
– значение 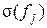 – значение
– значение 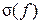 по (7) для частоты fj.
по (7) для частоты fj.
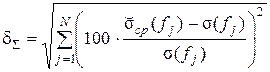 , %.
, %.


