Стоимость денег во времени. Дисконтирование
Одной из основных причин возникновения специальных методов оценки инвестиционных проектов является неодинаковая ценность денежных средств во времени. Практически это означает, что рубль сегодняшний считается нетождественным рублю через год. Причина такого разного отношения к одной и той же денежной сумме даже не инфляция, хотя мысль о ней может возникнуть в первую очередь. Куда более фундаментальной причиной является то, что рубль, вложенный в любого рода коммерческие операции (включая и простое помещение его на депозит в банке), способен через год превратиться в большую сумму за счет полученного с его помощью дохода. Предположим, что мы сегодня можем положить 1 000 руб. на депозит под 5% годовых. Через год сумма на сберегательном счете составит 1 050 руб. В нашем примере будущая стоимость (future value или FV) сегодняшних 1 000 руб. при ставке 5% годовых составит 1 050 руб. Если мы не будем изымать деньги из банка и оставим их там на второй и третий годы, то окончательная сумма после завершения двухлетнего и трехлетнего периода соответственно составит: Эта модель умножения сбережений, известная как модель сложных процентов, в общем виде может быть записана следующим образом: где FV – будущая величина той суммы, которую мы инвестируем в любой форме сегодня и которой будем располагать через интересующий нас период времени, в течение которого эти деньги будут работать; PV (present value) – текущая (современная) величина той суммы, которую мы инвестируем ради получения дохода в будущем; E – величина доходности наших инвестиций, в данном примере она равна ставке банковского процента по сберегательному вкладу, а в более общем случае – прибыльности инвестиций; к – число стандартных периодов времени, в течение которых наши инвестиции будут участвовать в коммерческом обороте, «зарабатывая» нам доходы. Как видно, из указанной формулы для расчета будущей стоимости (FV) мы применяем сложный процент. Это означает, что процент, начисленный на первоначальную сумму, прибавляется к этой первоначальной сумме и на него также начисляется процент. Если решить обратную задачу, т.е. определить текущую (современную) стоимость (PV) (или определение того, сколько надо было бы инвестировать сегодня, чтобы получить некоторую сумму в будущем). Для осуществления такого расчета используется формула, которая является обратной по смыслу формуле (2.3): PV = Следовательно, текущая (современная) стоимость равна будущей стоимости, умноженной на коэффициент В нашем примере текущая стоимость (PV) 1000 руб., которые будут получены через 3 года при 5% годовых, составит Определяя величину текущей стоимости (PV), исходя из суммы будущей стоимости, мы проводим дисконтирование будущей стоимости. Дисконтированием называется процесс приведения будущей стоимости денег к их текущей (современной стоимости). Процесс обратный дисконтированию, а именно, определение будущей стоимости, есть ни что иное, как начисление сложных процентов на первоначально инвестируемую стоимость. Коэффициенты дисконтирования не требуется каждый раз считать отдельно, они приводятся в специальных таблицах (если невозможно применение специального программируемого калькулятора). Дисконтированием денежных потоков называется приведение их разновременных (относящихся к разным шагам расчета) значений к их стоимости на определенный момент времени, который называется моментом приведения и обозначается через t0. Момент приведения может не совпадать с базовым моментом (началом отсчета времени, t0). Процедуру дисконтирования мы понимаем в расширенном смысле, т.е. как приведение не только к более раннему моменту времени, но и к более позднему (в случае, если t0>0). В качестве момента приведения наиболее часто (но не всегда) выбирают либо базовый момент (t0 = t0), либо начало периода, когда в результате реализации инвестиционного проекта предприятие начнет получать чистую прибыль. Основным экономическим нормативом, используемым при дисконтировании, является норма дисконта (E), выражаемая в долях единицы или в процентах в год. Дисконтирование денежного потока на m–м шаге осуществляется путем умножения его значения ЧДПm (CFm) на коэффициент дисконтирования рассчитываемый по формуле где tm – момент окончания m-го шага расчета, E выражена в долях единицы в год, а tm - t0 – в годах. Формула (2.5) справедлива для постоянной нормы дисконта, т.е. когда E неизменна в течение экономического срока жизни инвестиций или горизонта расчета. Норма дисконта (Rate of Dicount) – с экономической точки зрения это норма прибыли, которую инвестор обычно получает от инвестиций аналогичного содержания и степени риска. Таким образом, это ожидаемая инвестором норма прибыли (Opportunity Rate of Return). Норма дисконта (E) является экзогенно задаваемым основным экономическим нормативом, используемым при оценке эффективности ИП. В отдельных случаях значение нормы дисконта может выбираться различным для разных шагов расчета (переменная норма дисконта), это может быть целесообразно в случаях: - переменного по времени риска; - переменной по времени структуры капитала при оценке коммерческой эффективности ИП; - переменной по времени ставке процента по кредитам и др. Различаются следующие нормы дисконта: - коммерческая; - участника проекта; - социальная; - бюджетная. Коммерческая норма дисконта (E) используется при оценке коммерческой эффективности проекта; она определяется с учетом альтернативной эффективности использования капитала. Иными словами, коммерческая норма дисконта – это желаемая (ожидаемая) норма прибыльности (рентабельности), т.е. тот уровень доходности инвестируемых средств, который может быть обеспечен при помещении их в общедоступные финансовые механизмы (банки, финансовые компании и т.п.), а не при использовании в данном инвестиционном проекте. Таким образом, E – это цена выбора (альтернативная стоимость) коммерческой стратегии, предполагающей вложение денежных средств в инвестиционный проект. Норма дисконта участника проекта отражает эффективность участия в проекте предприятий (или иных участников). Она выбирается самими участниками. При отсутствии четких предпочтений в качестве нее можно использовать коммерческую норму дисконта. Для оценки коммерческой эффективности проекта в целом зарубежные специалисты по управлению финансами рекомендуют применять коммерческую норму дисконта, установленную на уровне стоимости капитала. Говоря о стоимости капитала, мы должны знать, что она представляет собой цену выбора или альтернативную стоимость его использования (opportunity cost). Это вызвано тем, что деньги – это один из видов ограниченных (экономических) ресурсов, а потому, направляя их на финансирование одного типа коммерческих операций, мы делаем невозможным вложение этих средств в другие виды деятельности. Следовательно вложение средств оказывается оправданным только в том случае, если это приносит доход больший, чем по альтернативным проектам с тем же уровнем риска. Если инвестиционный проект осуществляется за счет собственного капитала фирмы, то коммерческая норма дисконта, используемая для оценки коммерческой эффективности проекта в целом, может устанавливаться в соответствии с требованиями к минимально допустимой будущей доходности вкладываемых средств, определяемой в зависимости от депозитных ставок банков первой категории надежности. При экономической оценке инвестиционных проектов, осуществляемых за счет заемных средств, норма дисконта принимается равной ставке процента по займу. Поскольку в большинстве случаев привлекать капитал приходится не из одного источника, а из нескольких (собственный капитал и заемный капитал), то обычно стоимость капитала формируется под влиянием необходимости обеспечить некий усредненный уровень прибыльности. Поэтому средневзвешенная стоимость капитала WACC (Weighted Average Cost of Capital) может быть определена как тот уровень доходности, который должен приносить инвестиционный проект, чтобы можно было обеспечить получение всеми категориями инвесторов дохода, аналогичного тому, что они могли бы получить от альтернативных вложений с тем же уровнем риска. В этом случае WACC формируется как средневзвешенная величина из требуемой прибыльности по различным источникам средств, взвешенной по доле каждого из источников в общей сумме инвестиций. Общая формула для определения средневзвешенной стоимости капитала имеет следующий вид: WACC = где n – количество видов капиталов; E – норма дисконта i–го капитала; di – доля i–го капитала в общем капитале.
|

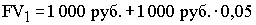 ,
,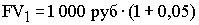 ,
,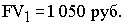


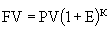 , (2.3)
, (2.3) . (2.4)
. (2.4) , называемый коэффициентом дисконтирования.
, называемый коэффициентом дисконтирования.
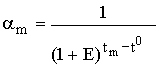 , (2.5)
, (2.5)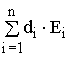 , (2.6)
, (2.6)


