Модель общего равновесия Вальраса. Вывод условий первого порядка.
Рассмотрим экономику, в которой производится n видов продукции с помощью m факторов производства. Обозначим через p = (p1,…,pn)T – вектор цен выпуска, w = (w1,…,wn)T – вектор цен факторов производства. Будем предполагать, что рынок функционирует в условиях совершенной конкуренции. Будем предполагать, что на рынке присутствует k фирм, каждая из которых способна выпускать любой из видов продукции, осуществляя затраты факторов производства. Обозначим через q(i)=(q1(i),….,qn(i))T вектор выпуска продукции i-й фирмой, через x(i)=(x1(i),….,xm(i))T вектор затрат факторов производства i-й фирмы. Производственную функцию фирм запишем в неявном виде:
Как и раньше будем предполагать, что фирмы максимизируют свою прибыль с учетом собственной технологии производства. Тогда задачи фирм будут выглядеть следующим образом:
Функция Лагранжа имеет следующий вид:
Условия первого порядка будут иметь следующий вид:
Каждая система содержит n + m + 1 уравнение с n + m + 1 неизвестным. Поскольку эти уравнения справедливы для каждой из k фирм, то имеем (n+m+1)k уравнений для решения задачи общего равновесия. Кроме этого, в экономике имеется l потребителей, каждый из которых владеет определенным фактором производства, который он может продать на рынке ресурсов и получить доход. Кроме того, предполагается, что потребитель получает определенную долю прибыли каждой фирмы. Обозначим через h(i)=(h1(i),….,hn(i))T набор товаров, приобретаемый i-м потребителем, через y(i)=(y1(i),….,ym(i))T набор факторов производства, находящийся в распоряжении i-го потребителя, через s(i)=(s1(i),….,sk(i))T - вектор долей участия i-го потребителя в прибылях фирм. Тогда функция полезности i-го потребителя имеет вид:
Бюджетное ограничение потребителей принимает вид:
где Задачи потребителей принимают вид:
Функция Лагранжа имеет следующий вид:
где Условия первого порядка будут иметь следующий вид:
Каждая система содержит n + m + 1 уравнение с n + m + 1 неизвестным. Поскольку эти уравнения справедливы для каждого из l потребителей, то имеем (n+m+1)l уравнений для решения задачи общего равновесия.
|

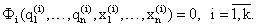 (в х коэффициент m)
(в х коэффициент m)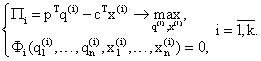 (вместо с пишем w, и можно сократить q(i)T и x(i)T)
(вместо с пишем w, и можно сократить q(i)T и x(i)T)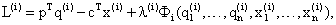 (в лямбда в скобках i-ые элементы и лямбда, вместо с пишем w, и сворачиваем Ф в скобках до векторов)
(в лямбда в скобках i-ые элементы и лямбда, вместо с пишем w, и сворачиваем Ф в скобках до векторов)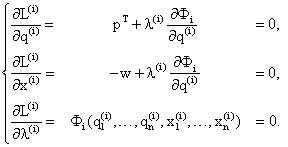 (w имеет транспонировки знак)
(w имеет транспонировки знак)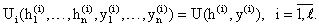 (знаки Т)
(знаки Т)
 - вектор прибыли фирм.
- вектор прибыли фирм.
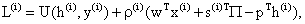
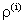 – множитель Лагранжа для
– множитель Лагранжа для 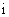 -го потребителя.
-го потребителя.



