Эффект Холла
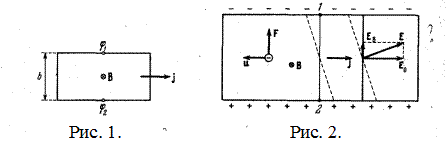
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля, возникает разность потенциалов Холловская разность потенциалов определяется выражением
Здесь Эффект Холла очень просто объясняется электронной теорией. В отсутствие магнитного поля ток в пластинке обусловливается электрическим полем При включении магнитного поля каждый носитель оказывается под действием магнитной силы F, направленной вдоль стороны Ь пластинки и равной по модулю
В результате у электронов появляется составляющая скорости, направленная к верхней (на рисунке) грани пластинки. У этой у грани образуется избыток отрицательных, соответственно у нижней грани — избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле
Поле
прежде лежали на одной и той же эквипотенциальной поверхности, теперь имеют разные потенциалы. Чтобы найти напряжение, возникающее между этими точками, нужно умножить расстояние между ними
Выразим и через
Последнее выражение совпадает с (1), если положить
Из (4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носителей в единице объема). Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электрического поля, равной единице. Если в поле напряженности Е носители приобретают скорость и, то подвижность их
Подвижность можно связать с проводимостью
Измерив постоянную Холла Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к п- или р-типу. На рис. 3 сопоставлен
эффект Холла для образцов с положительными и отрицательными носителями. Направление магнитной силы изменяется на противоположное как при изменении направления движения заряда, так) и при изменении его знака. Следовательно, при одинаковом направлении тока и поля магнитная сила, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (на рисунке) грани выше, чем нижней, а в случае отрицательных носителей—ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока. Любопытно, что у некоторых металлов знак
|

 (рис. 1). Это явление было обнаружено Холлом в 1879 г. и называется эффектом Холла или гальваномагнитным явлением.
(рис. 1). Это явление было обнаружено Холлом в 1879 г. и называется эффектом Холла или гальваномагнитным явлением. (1)
(1)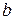 — ширина пластинки,
— ширина пластинки,  — плотность тока, В — магнитная индукция поля, R — коэффициент пропорциональности, получивший название постоянной Холла.
— плотность тока, В — магнитная индукция поля, R — коэффициент пропорциональности, получивший название постоянной Холла. (рис. 2). Эквипотенциальные, поверхности этого поля. образуют систему перпендикулярных к вектору
(рис. 2). Эквипотенциальные, поверхности этого поля. образуют систему перпендикулярных к вектору  (2)
(2) . Когда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2), установится стационарное распределение зарядов в поперечном направлении. Соответствующее значение
. Когда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2), установится стационарное распределение зарядов в поперечном направлении. Соответствующее значение 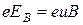 . Отсюда
. Отсюда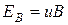
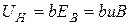
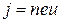 . В результате получим
. В результате получим (3)
(3)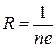 (4)
(4) равна
равна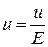 (5)
(5)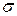 и концентрацией носителей п. Для этого разделим соотношение
и концентрацией носителей п. Для этого разделим соотношение 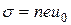 (6)
(6)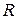 и проводимость
и проводимость 
 соответствует положительным носителям тока. Объяснение этой аномалии дает квантовая теория.
соответствует положительным носителям тока. Объяснение этой аномалии дает квантовая теория.


