III Задачі
Модуль 5 Вектори і координати ЗМ 14 Вектори у просторі. Дії над векторами
Мета: формування знань про вектори в просторі, дій над векторами, поняття кута між векторами, скалярного добутку векторів вмінь застосовувати вивчений матеріал до розв'язування задач
I Опорні питання заняття: 1 Вектори у просторі. 2 Дії над векторами у просторі. 3 Розкладання вектора на складові. II Запитання для самоперевірки III Задачі
Ключові поняття: вектор, координати вектора, довжина вектора, колінеарність, нуль-вектор, орт-вектор, скалярний добуток векторів, кут між векторами
Література: Ø Погорєлов О.В. Стереометрія: Підруч. для 10-11 кл. серед. шк. Ø Бевз Г.П. та ін. Геометрія: Підруч. для 10-11 кл. загальноосв.навч.закл.
I Опорні питання заняття: 1 Вектором називається напрямлений відрізок Координатами вектора називаються різниці координат кінця і початку вектора. Нехай координати точок
Координати вектора не змінюються при паралельному перенесенні. У рівних векторів однакові і координати.
Модулем (абсолютною величиною, довжиною) вектора називається довжина відрізка, яким задається вектор.
Згадайте, за якою формулою знаходять довжину відрізка, якщо його кінці задані певними координатами?
Нульовим вектором (нуль-вектором) називається вектор, кінець якого співпадає з початком. Зображується такий вектор точкою і позначається Колінеарними називаються вектори, які лежать на одній прямій або на паралельних прямих. Нуль-вектор вважається колінеарним довільному вектору.
|

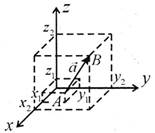 Вектори у просторі
Вектори у просторі
 і
і 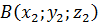 , тоді координати вектора
, тоді координати вектора 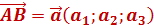 , де
, де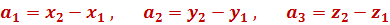
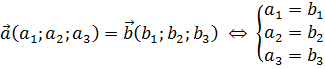
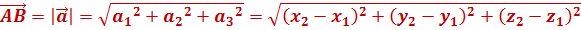
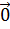 . Модуль такого вектора дорівнює нулю, а його напрям невизначений.
. Модуль такого вектора дорівнює нулю, а його напрям невизначений.


