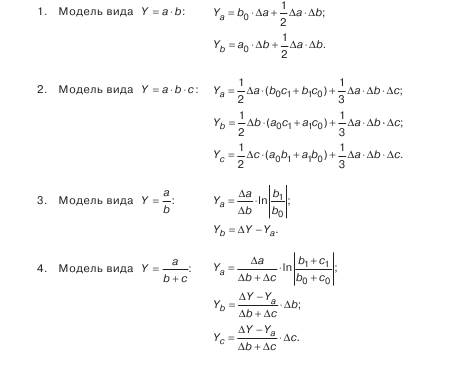Элиминирование как способ детерминированного факторного анализа имеет важный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели. Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида.
Использование этого способа позволяет получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния: в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну.
Для распределения дополнительного прироста недостаточно взять его часть, соответствующую количеству факторов, т. к. факторы могут действовать в разных направлениях. Поэтому изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках. В связи со сложностью вычисления некоторых определенных интегралов и дополнительные сложностей, связанных с возможным действием факторов в противоположных направлениях, на практике используются специально сформированные рабочие формулы, приводимые в специальной литературе:
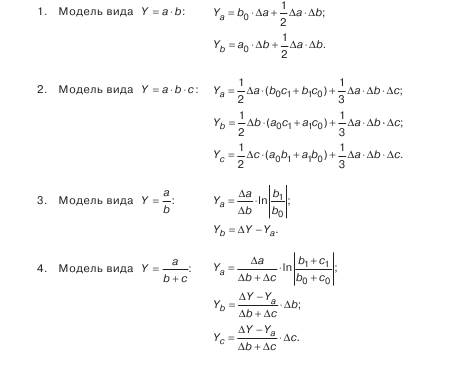
Таким образом, использование интегрального метода не нуждается в знании всего процесса интегрирования. Достаточно лишь в рабочие формулы подставить необходимые числовые данные и сделать подсчеты. При этом достигается более высокая точность расчетов.