СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайные события удобно связывать с действительными числами и вместо действий над событиями проводить действия над числами. Случайной называют величину, которая при повторении опыта может принимать неодинаковые числовые значения, причем заранее неизвестно какие. Случайная величина называется дискретной, если ее множество значений конечно или счетно. Случайная величина называется непрерывной, если ее значения целиком заполняют некоторый интервал. Случайные величины будем обозначать большими буквами ( Законом распределения называют соотношение вида Интегральной функцией распределения (или интегральным законом распределения) называют функцию
Интегральная функция распределения Свойства функции распределения 1) 2) 3) из этих свойств следует, что Функцию распределения дискретной случайной величины можно построить, если известен ряд распределения
Для непрерывной случайной величины вводится функция плотности вероятности (плотность распределения, дифференциальный закон распределения)
Выразим вероятность попадания величины
Пусть
Эта формула выражает функцию распределения Свойства функции плотности вероятности 1) 2) Для случайных величин были введены полные исчерпывающие характеристики, для дискретной случайной величины - функция распределения
В практических задачах часто нет необходимости характеризовать случайную величину полностью и достаточно ограничиться указанием отдельных числовых параметров, которые характеризуют существенные особенности распределения. Такие характеристики называют числовыми характеристиками. Числовые характеристики дискретной случайной величины 1) математическое ожидание
2) дисперсия
3) среднеквадратическое отклонение
Числовые характеристики непрерывной случайной величины: 1) математическое ожидание
2) дисперсия
3) среднеквадратическое отклонение
|

 ), а их возможные значения соответственно малыми буквами (x). Если проведен опыт, в котором случайная величина
), а их возможные значения соответственно малыми буквами (x). Если проведен опыт, в котором случайная величина 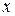 , то
, то  . Вероятности этих событий обозначим
. Вероятности этих событий обозначим  , …,
, …,  . Очевидно, что
. Очевидно, что  .
.
 . Если закон распределения задан таблицей, то таблицу называют рядом распределения (см. пример 15), если закон распределения задан графиком, то его называют многоугольником распределения. Закон распределения существует только для дискретных случайных величин, т.к. возможные значения непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
. Если закон распределения задан таблицей, то таблицу называют рядом распределения (см. пример 15), если закон распределения задан графиком, то его называют многоугольником распределения. Закон распределения существует только для дискретных случайных величин, т.к. возможные значения непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток. .
.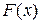 является универсальной характеристикой случайной величины, она существует и для дискретной случайной величины и для непрерывной случайной величины.
является универсальной характеристикой случайной величины, она существует и для дискретной случайной величины и для непрерывной случайной величины.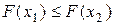 при
при 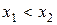 ;
; ;
;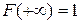 ;
;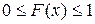 .
.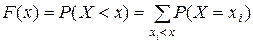 , суммирование распространяется на все те значения
, суммирование распространяется на все те значения  , которые меньше
, которые меньше  ,
, .
.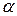 до
до  :
: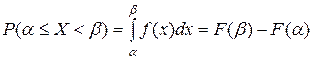 .
.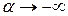 ,
,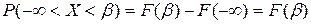 (
(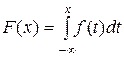 .
. . Графики функций
. Графики функций  приведены в примере 16.
приведены в примере 16.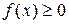 ;
;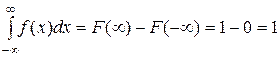 .
. ;
;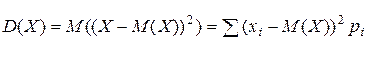 ;
; .
.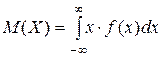 ;
;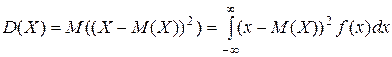 .
.


