ЛОКАЛЬНАЯ И ИНТЕГРАЛЬНАЯ
ФОРМУЛЫ МУАВРА – ЛАПЛАСА При достаточно большом
Эта формула также табулирована (приложение табл. 3), Вероятность того, что при указанных условиях событие А появится не менее
где Функция Лапласа представляет собой не выражающийся через элементарные функции интеграл. Значения функции Лапласа приведены в приложении табл. 4. Свойства функции Лапласа: 1) функция монотонно возрастает, т.е. 2) 3) функция Лапласа является нечетной 4) значения функции приближаются к асимптотическому значению при
|

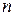 и не слишком малых
и не слишком малых 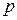 и
и  (
( ,где
,где  ,
,  .
. .
.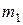 и не более
и не более  раз, находится по интегральной формуле Муавра – Лапласа:
раз, находится по интегральной формуле Муавра – Лапласа: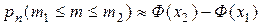 ,
, ,
,  ,
,  ,
,  - функция Лапласа.
- функция Лапласа. при
при 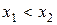 ;
;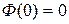 ,
, 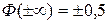 ;
; .
.
 .
.


