Решение некоторых гидродинамических задач притока жидкости к горизонтальным стволам скважин на основе теории функций комплексного переменного.
За последнее время с целью наиболее полного извлечения нефти из продуктивного пласта нашло применение горизонтальных стволов скважин и в особенности при наличии подошвенной воды. При этом возникает необходимость в построении достаточно приемлемых аналитических решений задач притока жидкости к горизонтальным стволам и реализации их для практического промыслового использования: определения предельных безводных дебитов и депрессий; определения безводного периода эксплуатации скважин и текущего коэффициента нефтеизвлечения в удельном объеме дренирования; оценка возможности совместно-раздельного отбора нефти и воды и др. Кроме того, если будет известна скорость продвижения поверхности раздела двух жидкостей (конуса подошвенной воды), то проявится возможность установить оптимальную технологию добычи нефти, т. е. определить соответствующие расстояния между стволами (выбрать сетку горизонтальных стволов), темпы отбора нефти продолжительность безводного периода эксплуатации скважин. Впервые теория функций комплексного переменного применена к плоским задачам теории фильтрации М. Маскетом [56] и И. А. Чарным [2], которые получили следующие уравнения для функции потенциала
Здесь
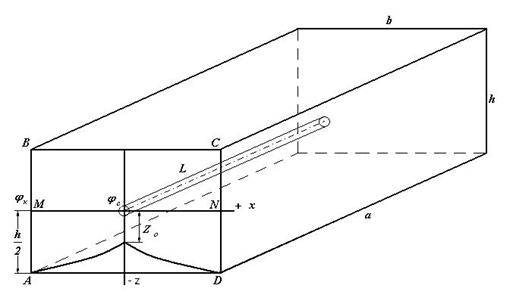
Рис. 13.8.1. Схема расположения горизонтального ствола в
|

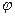 скорости фильтрации и функции линий тока
скорости фильтрации и функции линий тока 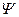 соответственно:
соответственно: , (13.8.1)
, (13.8.1)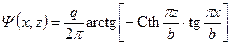 . (13.8.2)
. (13.8.2) – мощность точечного стока, лежащего в центре расчетного блока с координатами по вертикальному сечению пласта
– мощность точечного стока, лежащего в центре расчетного блока с координатами по вертикальному сечению пласта  , м2/с (рис. 13.8.1; горизонтальный ствол (линия стоков) лежит в плоскости
, м2/с (рис. 13.8.1; горизонтальный ствол (линия стоков) лежит в плоскости  );
); – ширина расчетного блока (расстояние между стволами);
– ширина расчетного блока (расстояние между стволами); – гиперболический косинус;
– гиперболический косинус; – гиперболический котангенс;
– гиперболический котангенс;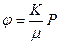 – потенциал скорости фильтрации (
– потенциал скорости фильтрации ( – коэффициент проницаемости по напластованию;
– коэффициент проницаемости по напластованию;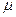 – коэффициент абсолютной вязкости;
– коэффициент абсолютной вязкости;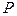 – давление в любой точке пласта).
– давление в любой точке пласта).