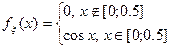Часть II.
За каждое правильно выполненное задание даётся один балл, в противном случае баллы не начисляются. 1. В коробке 7 деталей, из которых 4 – бракованы. Наудачу извлекли без возврата 2 детали, тогда вероятность что обе детали бракованы А). 2/7 Б). 4/7 В). 2/4 Г). 1/2 2. В условиях предыдущей задачи вероятность, что хотя бы одна деталь бракована: А). 2/7 Б). 4/7 В). 6/7 Г). 1/2 3. В условиях предыдущей задачи вероятность, что вторая деталь бракована: А). 2/7 Б). 4/7 В). 2/4 Г). 1/2 4. По мишени независимо стреляют по одному разу два стрелка - A и B с вероятностями попадания Р(А)=0.6, Р(В)=0,7. Тогда A). 0.18 Б). 0.1 В). –0.2 Г). 0.5 5. В урне 15 чёрных шаров и 6 – белых. Наудачу берут один шар. Вероятность, что он белый: A). 2/7 Б). 3/7 В). 1 Г). 4/5. 6. Вероятность попадания в мишень из пистолета А равна 0.7, из пистолета В – 0.9. Из наудачу взятого пистолета выстрелили. Вероятность попадания равна: A). 0.8 Б). 0.6 В). 0.46 Г). 0. 7. В условиях предыдущей задачи в мишень попали, то вероятность что это был пистолет А равна: A). 2/7 Б). 7/16 В). 1 Г). 0. 8. Буквы слова ТАРАКАН рассыпаны в беспорядке. Вероятность того что, беря наудачу 4 буквы подряд, получим слово ТАРА равна: A). 1/280 Б). 0 В). 1/140 Г). 0.5 9. Вероятность попадания при одном выстреле равна 0.8. Произведено 3 выстрела. Вероятность ровно двух попаданий равна: A). 0.384 Б). 0 В). 1 Г). 0.5 10. В большой коробке белых и чёрных шаров поровну. Вероятность взять наудачу 2 чёрных равна: A). 0.25 Б). 3/4 В). 1 Г). 0.5 11. На автостраде легковые и грузовые машины встречаются как 1:3. Вероятность попасть в аварию для легкового 0.2, для грузового – 0.1. Вероятность аварии на автостраде равна A). 0.125 Б). 0.4 В). 0.5 Г). 0.12 12. В условиях предыдущей задачи - произошла авария. Вероятность, что это был грузовик равна: A). 0.12 Б). 0.4 В). 0.5 Г). 0.6 13. Стрелок имеет два патрона и стреляет до первого попадания. Вероятность попадания при одном выстреле равна 0.8, Х – число выстрелов, тогда М(Х) равно A). 0.12 Б). 0.4 В). 0.5 Г). 1.12 14. Если M(X)=2, то M(3X-5) равно: А. 4 Б. 3 В. 1 Г. -2. 15. Если D(X)=2, D(Y)=3 и случайные величины X и Y независимы, то D(2X-Y) равно: А. 4 Б. 11 В. 7 Г. 1. 18. Функция распределения имеет вид: А. В.
19. Дано распределение случайных величин X и Y. Тогда D(Y) равно
А.0.24 Б. 1 В. 0 Г. –1 20. В условиях предыдущей задачи M(X) равно А. 1.4 Б.1.6 В. 1 Г. –1
|

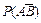 равна:
равна: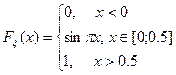 . Тогда fξ(x) равна
. Тогда fξ(x) равна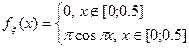 Б.
Б. 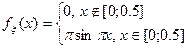
 Г.
Г.