Тест № 0
для студентов заочного факультета II курса, III семестр. За каждое правильно выполненное задание начисляется один балл, в противном случае – ноль баллов. I. Пусть A, B и C – случайные события, Ω – достоверное событие, тогда: 1. A(B+C)=AB+BC 2. A+B Ì A 3. II. Пусть A, B – случайные события и P(A), P(B) – их вероятности, тогда 5. P(A+B)=P(A)+P(B) 6. P(AB)=P(A)P(B) 7. AÌ B Þ P(A+B)=P(A) 8. III. Пусть X, Y – случайные величины, тогда: 9. M(X+Y)=M(X)+M(Y) 10. M(XY)=M(X)M(Y) 11. D(X+Y)=D(X)+D(Y) 12. D(XY)=D(X)D(Y) IV. Пусть 13. V. Пусть 17. VI. Справедливы следующие утверждения: 21. Если случайные события A и B независимые, то P(AB)=P(A)P(B). 22. Если случайные события A и B образуют полную группу несовместных событий, то для любого события C P(C)=P(A)P(C|A)+P(B)P(C|B).
|

 4.
4. 
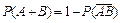
 – функция распределения случайной величины ξ, тогда:
– функция распределения случайной величины ξ, тогда: 14.
14. 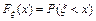 15.
15.  16.
16.  – функция плотности распределения случайной величины ξ, тогда:
– функция плотности распределения случайной величины ξ, тогда: 18.
18.  19.
19.  20.
20. 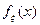 – возрастающая ф-ция.
– возрастающая ф-ция.


