Вероятность появления хотя бы одного события. Пусть события A1, A2, , An независимы в совокупности, причем
Пусть события A1, A2,..., An независимы в совокупности, причем P (A1) = p1, P (A2) = p1, …, P (An) = pn; пусть в результате испытания могут наступить все события, либо часть из них, либо ни одно из них. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий A1, A2,..., An независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Р (А) = 1 – q1q2 … qn. В частности, если все n событий имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий Р (А) = 1 – qn.
|

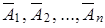 :
:


