Применение элементов комбинаторики к нахождению вероятностейОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ Классическое определение вероятности Относительная частота и статистическая вероятность Геометрические вероятности ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Теоремы сложения и умножения вероятностей Формула полной вероятности Формула Бейеса ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ Формула Бернулли ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Классическое определение вероятности
При классическом определении вероятность события определяется равенством Р(А)=т/п, где m – число элементарных исходов испытания, благоприятствующих появлению события А; п – общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.
Применение элементов комбинаторики к нахождению вероятностей
При вычислении вероятностей пользуются формулами теории соединений. Основными из них являются формулы для определения: Pk – числа перестановок из k элементов,
Число перестановок из k элементов равно:
где Например: сколько трёхзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз. Искомое количество трёхзначных чисел Число размещений из k элементов по s равно:
Например: сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2. Искомое число сигналов Число сочетаний из k элементов по s равно:
Например: сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей. Искомое число способов
|
– числа размещений из k элементов по s,
– числа сочетаний из k элементов по s.
,
. Принято, что 0!=1.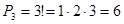
.
.
.
.
.
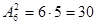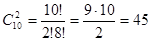