Группа 2 видаНеизвестными являются: величины и направления векторов реакций в шарнирах A и B; величина и точка приложения реакции в поступательной паре. Реакцию во внешнем шарнире A раскладываем на составляющие (рис. 4.5); реакцию в поступательной паре направляем перпендикулярно направляющей 4 и обозначаем для нее плечо относительно оси
Для определения искомых величин выполняем следующие действия: 1) составляем уравнение моментов всех сил, действующих на звено 2, относительно оси шарнира B; в этом уравнении участвует только одна неизвестная – 2) составляем векторное уравнение плана сил для группы:
в это уравнение не входит реакция из (4.4) находим составляющую реакции 3) составляем уравнение моментов сил, действующих на звено 3, относительно оси шарнира B; решая его, находим алгебраическое значение 4) составляем векторное уравнение плана сил для звена 3:
решая которое, находим величину и направление реакции В результате расчета группы найдены все требуемые условием величины.
|
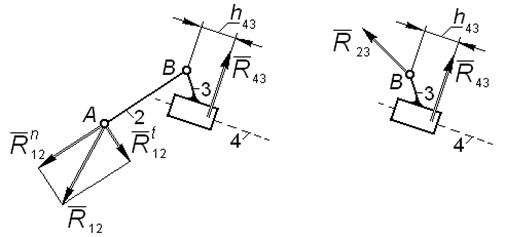
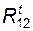, которая и определяется как алгебраическая величина;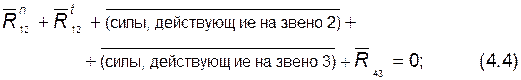
(или 
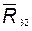) в шарнире B;
(а следовательно, и полную реакцию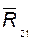 
) и реакцию в поступательной паре 
;
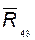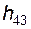– плеча реакции 
