Определение периода полураспада для смеси двух радиоактивных изотопов
а) Рассчитать средний фон счетной установки (
где i – номер измерения, в данном случае может принимать значения 1, 2, 3; I – количество измерений фона, в данном случае равно 3; б) Определить среднее значение скорости счета (
в) Определить среднее значение скорости счета в момент времени t, обусловленного только активностью индиевого образца (
г) Определить среднее значение активности индиевого образца и его погрешность по соотношениям:
д) Период полураспада второго изотопа составляет около 24 с, это значит, что через 240 с около 99,9% этого радиоактивного изотопа распадется. Поэтому в интервале времени
е) Построить график зависимости активности образца от времени в полулогарифмическом масштабе ( ж) Определяется среднее значение логарифма активности, обусловленной первым изотопом, в моменты времени
з) Определяется среднее значение активности, обусловленной первым изотопом, в моменты времени
и) Определяется среднее значение активности, обусловленной вторым изотопом, и его погрешность (
к) Определяется среднее значение логарифма активности, обусловленной вторым изотопом, и его погрешность (
Рис. 2.3. Пример обработки зависимости активности образца от времени в полулогарифмическом масштабе для долгоживущего изотопа
л) Построить график зависимости активности образца от времени в полулогарифмическом масштабе ( м) По тангенсу угла наклона прямых линий определить два предельных значения постоянной распада (λ;1, λ;2) для долго- и короткоживущего изотопов по соотношениям:
где н) Определить среднее значение постоянной распада (
о) Определить среднее значение периода полураспада (
п) Составить отчет о выполненной работе, который должен включать следующее: − самостоятельно сформулированную цель работы; − необходимые теоретические сведения; − результаты измерений и расчеты необходимых величин со своими погрешностями (таблица № 2.4); − необходимые зависимости; − вывод по работе.
|

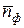 ) и погрешность его измерения (
) и погрешность его измерения ( ) по соотношениям:
) по соотношениям: ;
;  ,
, – скорость счета фона в i -ом измерении.
– скорость счета фона в i -ом измерении. ) и его погрешность (
) и его погрешность (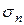 ). В данном случае на каждый момент времени t имеется одно измерение, поэтому используются следующие соотношения (см. раздел 1):
). В данном случае на каждый момент времени t имеется одно измерение, поэтому используются следующие соотношения (см. раздел 1): ;
;  .
. ), т.е из всех полученных замеров исключить фон и оценить его погрешность (
), т.е из всех полученных замеров исключить фон и оценить его погрешность (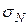 ) по соотношениям:
) по соотношениям: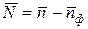 ;
; 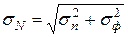 .
. ;
; 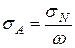 .
. мин активность обусловлена только первым радиоактивным нуклидом с периодом полураспада около 2,42 мин. Для определения его постоянной распада необходимо в интервале времени
мин активность обусловлена только первым радиоактивным нуклидом с периодом полураспада около 2,42 мин. Для определения его постоянной распада необходимо в интервале времени  ) и его погрешность (
) и его погрешность (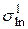 ) по соотношениям:
) по соотношениям: ;
;  .
.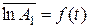 ). Для этого на график наносятся экспериментальные значения
). Для этого на график наносятся экспериментальные значения 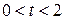 мин и графически определяются значения логарифмов активности, обусловленной первым изотопом, в моменты времени
мин и графически определяются значения логарифмов активности, обусловленной первым изотопом, в моменты времени 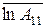 ) и второй прямой (
) и второй прямой (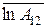 ) (рис. 2.3).
) (рис. 2.3). ;
;  .
. ) по соотношениям:
) по соотношениям: ;
; 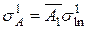 .
.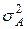 ) по соотношениям:
) по соотношениям: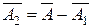 ;
; 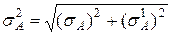 .
.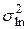 ) по соотношениям:
) по соотношениям: ;
; 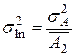 .
.
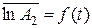 ). Для этого на график наносятся значения
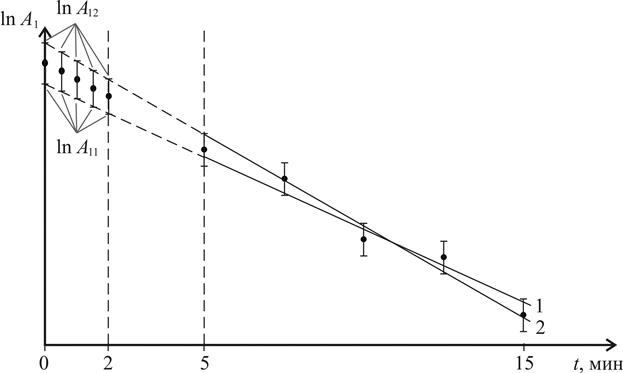
). Для этого на график наносятся значения  с доверительными интервалами в рамках которых строятся две прямые линии. Так как постоянная распада определяется по тангенсу угла наклона этих линий, то необходимо строить их в двух крайних по углу наклона положениях (“пологая” – 1 и “крутая” – 2 линии на рис. 2.2).
с доверительными интервалами в рамках которых строятся две прямые линии. Так как постоянная распада определяется по тангенсу угла наклона этих линий, то необходимо строить их в двух крайних по углу наклона положениях (“пологая” – 1 и “крутая” – 2 линии на рис. 2.2).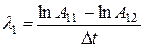 ;
;  ,
,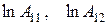 – значения логарифмов активности для “пологой” прямой 1 (рис. 2.2) в первой и второй точке соответственно;
– значения логарифмов активности для “пологой” прямой 1 (рис. 2.2) в первой и второй точке соответственно;  – значения логарифмов активности для “крутой” прямой 2 (рис. 2.2) в первой и второй точке соответственно.
– значения логарифмов активности для “крутой” прямой 2 (рис. 2.2) в первой и второй точке соответственно. ) и ее погрешность (
) и ее погрешность (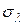 ) по соотношениям:
) по соотношениям: ;
; 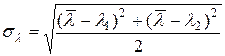 .
. ) и его погрешность (
) и его погрешность (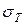 ) по соотношениям:
) по соотношениям: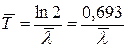 ;
;  .
.


