Общие сведения.Законы Ньютона и Пуазейля.
Вязкость жидкостей, к которым относят расплавы солей или металлов, является одним из их важнейших физико-химических свойств. Свойство вязкости связано со структурой жидкости и обусловлено межчастичным взаимодействием. От вязкости в известной степени зависит чистота получаемого металла по неметаллическим и шлаковым включениям и газосодержание расплава. Скорость удаления неметаллических частиц и пузырьков газа обратно пропорциональна вязкости жидкого металла. Вязкость определенным образом влияет на режим разливки, формирование структуры слитка, на заполняемость литейных форм. Существует корреляционная связь между вязкостью жидкого металла и процессом его кристаллизации, а следовательно, и свойствами твердого металла. Вязкость характеризует движение молекул под действием силы механического воздействия (сдвига) и представляет собой отклик системы на внешнее механическое воздействие, аналогично подвижности ионов или коэффициента седиментации на действие электрической или центробежной силы, соответственно. С другой стороны высокая вязкость обусловлена силами сцепления между молекулами жидкости. Довольно часто вязкость называют внутренним трением жидкости. Вязкость и текучесть жидкости относят к её реологическим свойствам. При протекании жидкости через трубку различные ее слои, располагающиеся концентрически от стенок трубки к ее центру, движутся с разной скоростью. У стенки слой жидкости неподвижен, а следующие слои движутся со все большей скоростью, но постоянной для каждого слоя. Такой поток называется ламинарным. Схематически это показано на рисунке 1.
ύ Рис.1.Зависимость скорости течения жидкости в трубке (ка- пилляре) с радиусом r для ла- минарного потока. r 0 r Зависимость скорости жидкости от положения внутри капилляра описывается простой параболой. При увеличении скорости слои образуют завихрения и перемешиваются, и тогда ламинарный поток переходит в турбулентный. Ламинарный (или слоистый) поток называют ньютоновским, а соответствующие жидкости ньютоновскими. Турбулентный поток называют неньютоновским, а соответствующие жидкости неньютоновскими. Ламинарное движение жидкости описывается двумя законами: законом Ньютона и законом Пуазейля. Закон Ньютона характеризует силу вязкого сопротивления жидкости (силу трения) F в соответствии с уравнением (1):
где: h - коэффициент динамической вязкости (или динамическая вязкость), S - площадь соприкосновения слоев жидкости, В соответствии с законом Ньютона сила трения пропорциональна градиенту скорости по расстоянию dx между слоями с площадью поверхности равной S. Поэтому абсолютная вязкость представляет собой в этом уравнении коэффициент пропорциональности (h), характеризующий внутреннее трение в среде при единичных значениях градиента скорости и площади поверхности соприкасающихся слоев жидкости. Кинематическая вязкость (коэффициент кинематической вязкости) жидкостей определяется по уравнению где: Из уравнений (1) можно определить размерность вязкости [h] в системе СИ:
В системе СГС: Соотношение между размерностями в разных системах:
В системе СИ размерность кинематической вязкости м2 /c, а в системе CГC единица кинематической вязкости называется стоксом (Ст). 1 Ст = 10-4 м2 /c. Абсолютная вязкость чистой воды при 200С равна Анатом Пуазейль, изучавший движение крови по кровеносным сосудам, установил, что расход крови (объем/время) протекающей по кровеносному сосуду (трубке) рассчитывается по уравнению:
где: V - объем жидкости (крови); t - время истечения жидкости из трубки, r - радиус трубки; Простым устройством для измерения вязкости является вискозиметр Оствальда (рис.2) с помощью которого измеряется время истечения определенного объема жидкости, ограниченного двумя рисками: ''а'' и ''б'', т.е. определяется скорость истечения жидкости. Учитывая, что давление столба жидкости пропорционально плотности жидкости r, вязкость жидкости можно определить по уравнению:
представляющему собой модифицированное уравнение Пуазейля
Действительно для данного вискозиметра Оствальда величины r, l и V являются неизменными. Учитывая, что P = k∙ρ в уравнении (4) где: k - коэффициент пропорциональности, получаем
Рис.2.Вискозиметр Оствальда Принимая h0, r0 и t0 в качестве соответствующих параметров для стандартной жидкости, например воды, из уравнения (5) можно получить основное уравнение метода вискозиметрии:
где: hx – вязкость; rx – плотность; tx - время истечения, соответственно, для исследуемого раствора. Исходя из уравнения (6) получаем:
Если раствор достаточно разбавленный, то его плотность rх не сильно отличается от плотности стандартной жидкости (растворителя), т.е. rх @ r0. Тогда уравнение (7) преобразуется в уравнение:
Из уравнения (8) следует, что для экспериментального определения вязкости жидкости hх достаточно определить с помощью вискозиметра Оствальда время истечения стандартной жидкости (например, воды), время истечения исследуемой жидкости и учесть вязкость стандартной жидкости. Законы Ньютона и Пуазейля перестают действовать при турбулентном движении жидкости. Поэтому оба закона применимы для чистых жидкостей, истинных растворов и некоторых коллоидных растворов. Вязкость жидких металлов зависит от их природы и закономерно уменьшается с повышением температуры. А.И. Бачинский установил зависимость между динамической вязкостью структурно однородной жидкости и её удельным объемом h = С / (V - B), (10) где: V-удельный объем (объем единицы массы), С и В – константы. Формула Бачинского характеризует зависимость вязкости от температуры поскольку удельный объем является функцией температуры. Как показал Я.И. Френкель температурная зависимость вязкости однородных жидкостей (политерма) выражается уравнением h = А· exp(Ea / RT), (11) где: А- постоянная, зависящая от природы жидкости, Ea – энергия активации вязкого течения - это минимальная энергия, необходимая для преодоления притяжения частиц своего слоя и перехода в другой слой. Экспериментальные данные показывают, что для многих чистых жидких металлов вязкость подчиняется экспоненциальной зависимости от температуры. В последнее время на политермах вязкости чистых жидких металлов обнаружены аномалии, свидетельствующие о структурных изменениях в расплавах. Необходимо помнить, что реальная металлическая жидкость не является структурно однородной. Поэтому применение формулы Френкеля ограничено. В бинарных жидких металлических системах зависимость вязкости от состава связана с характером диаграмм состояния. Другими словами концентрационные зависимости вязкости (изотермы) отражают положение линий диаграмм. Эвтектическим концентрациям некоторых бинарных систем соответствуют минимумы кинематической вязкости, а некоторых – максимумы кинематической вязкости, соответствующие образованию химических соединений. Для экспериментального определения вязкости расплавленных металлов, являющихся слабовязкими жидкостями, широкое распространение получил метод крутильных колебаний тигля с расплавом. В этом методе экспериментально определяют период крутильных колебаний системы и логарифмический декремент затухания, представляющий собой логарифм отношения амплитуд двух последующих колебаний, измеренных через определенный промежуток времени.
|

 или (1а)
или (1а) (1б)
(1б) - градиент скорости течения, du - разность скоростей движения двух соседних слоев.
- градиент скорости течения, du - разность скоростей движения двух соседних слоев. (2)
(2)
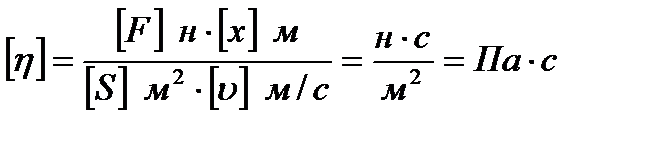
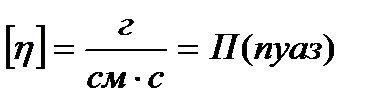
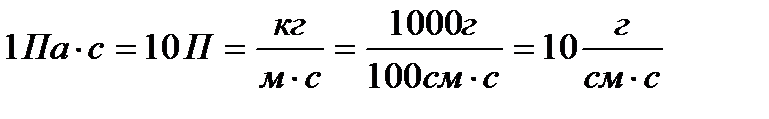
 .
. (3)
(3)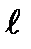 - длина трубки; Р - разность внешнего давления, действующего на протекающую жидкость на концах трубки, h - вязкость жидкости.
- длина трубки; Р - разность внешнего давления, действующего на протекающую жидкость на концах трубки, h - вязкость жидкости.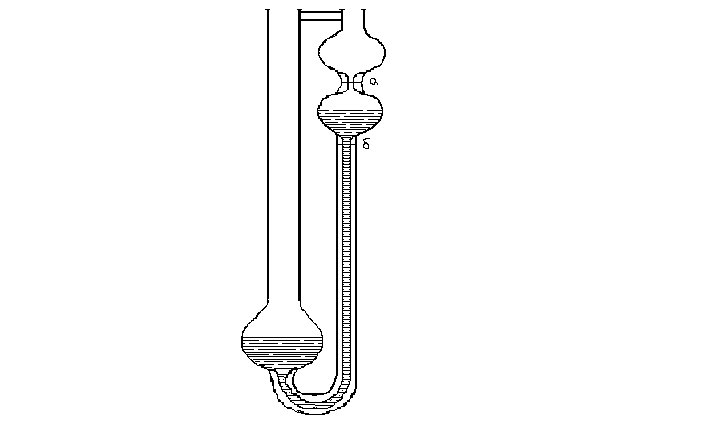
 , (4)
, (4)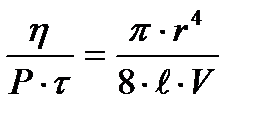 . (5)
. (5) (6)
(6)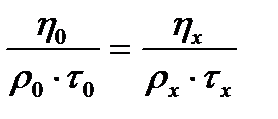 (7)
(7) (8)
(8)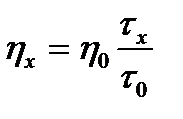 (9)
(9)


