В партии 29 образцов,из них 14 исправных. Наудачу отобрано 5 образцов
Решение:
1). Вероятность того, что среди отобранных образцов исправных ровно 3, вычисляется используя гипергеометрическое распределение =ГИПЕРГЕОМЕТ(…):
,где N - (размер совокупности), = 29; K - (число успехов в совокупности), = 14; n - (размер выборки), = 5; k - (число успехов в выборке), = 3. Вычисленная вероятность (того что среди отобранных образцов 3 исправных) равняется: P = 0,321839.
2). Всего имеется 29 образцов, известно что 14 из них исправны, следовательно остальные 15 не исправны. Так как выборка рана 5 образцам, то, если в нее попадут все не исправные образцы, число исправных образцов в выборке равняется 3.Отсюда следует, что необходимо рассчитать вероятность попадания в выборку от 3 до 5 исправных образцов для каждого случая в отдельности. Для этого в Excel,составляем и заполняем таблицу и опять используем гипергеометрическое распределение:
4). Функция распределения – это вероятность того, что случайная величина примет значение меньшее, чем конкретное числовое значение x чего получим:
По эти данным строим соответствующий график:
5). Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. Наибольшая вероятность в данном случае равна Р6 =0,321839, она соответствует вероятности попадания 6 исправных образцов. Следовательно, мода равна Mo(X) =0,3487. В Excel нахождение моды производилось по следующей формуле: ИНДЕКС(x;ПОИСКПОЗ(НАИБОЛЬШИЙ(p;1);p;0);1)
Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: M(x) = 4,7702. Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: Для вычисления дисперсии в Excel составляется следующая формула =СУММПРОИЗВ(X;X;Px)-М(х)*М(x). В результате чего, дисперсия равна: D(x) =6,622991. Среднее квадратичное отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: Для вычисления σx в Excel, из значения дисперсии извлекается квадратный корень, следующей функцией: КОРЕНЬ(D(x)). Среднее квадратичное отклонение равно: σx =2,573517.
Задание 2:
5 элементов соединены в цепь по следующей схеме:
Надежности элементов приведены в таблице:
1). Написать формулу для события Х=(цепь между узлами С и D проводит). 2). Рассчитать вероятность надежной работы цепи между узлами А и D, а также А и С.
Решение: Пусть Ei - надежность элемента, Ēi (= 1-Ei) – вероятность выхода из строя.
1). Составим и разберём схему цепи:
D 2 D
2 B B
2 B B B B
z8 = E3*E4 z7 = Z5 + Z8 = E5+E3*E 4 z6 = E2*z7 = E2*(E5+E3*E4) z = z1+z6 = E1+E2*(E5+E3*E4) → → Формула для события Х где цепь между узлами С и D равна: X=E1+E2*(E5+E3*E4).
2). Рассчитать вероятность надежной работы цепи между узлами А и В: · Участок DAB состоит из последовательно соединенных участков DA и AB, → P(DAB) = P(DA)*P(AB) = E1E2. · Участок DB состоит из параллельно соединенных участков DB и DAB, → P(DB) = P(DB) + P(DAB) – P(DB*DAB). P(DB*DAB) можно представить в виде P(DB)*P(DAB),(т.к. события независимы), → P(DB) = E5 + E1E2 – E5E1E2. · Участок DBC состоит из последовательно соединенных участков DB и BC, → P(DBC) = P(DB)*P(BC). P (BDC) = (E5 + E1E2 – E5E1E2)*E3. Нужный участок CD состоит из участков CD и DBC, которые связаны параллельно, → P(CD) = P(DBC)+ P(CD) –P(DBC)*P(CD). → Формула расчета надежности на участке СD равна: P(DC) = (E5+E1E2-E5E1E2)*E3+E43 – (E4+E1E2-E5E1E2)*E3*E4. В результате вычисления получим надежность P(BC) = 0,711.
Рассчитать вероятность надежной работы цепи между узлами А и В: В случае если участок DB работает, то для работы цепи нужно чтобы функционировал, хотя бы 1 из параллельно соединенных элементов участка BAD, и хотя бы 1 из параллельно соединенных элементов участка BCD. P(AC) = E5(E2+E3 – E2E3)(E1+E4 – E1E4). В случае если участок DB не работает то надежность цепи зависит от того работают ли параллельно соединенные участки ADC и ABC, каждый из которых состоящий из 2 последовательно соединенных элементов: P(AC) = Ē5(E1E2+E3E4 – E1E2E3E4). Общая формула для расчета надежности: P(AC) = E5(E2+E3 – E2E3)(E1+E4 – E1E4) – Ē5(E1E2+E3E4 – E1E2E3E4)
В результате вычислений получим, что P(AC) = 0,74.
Задание 3:
Вкладчик сделал вклады суммой S под процент r с риском обанкротиться p в 3 банка:
Построить ряд распределения для СВ S =( cyммaна всех счетах) и соответствующую гистограмму. Вычислить характеристики распределения: мат. ожидание, дисперсию, среднеквадратичное отклонение и среднее абсолютное отклонение.
Решение: Вычислим "Сумму вкладов через год",в каждом банке по отдельности. Она рано вложенной сумме денег плюс проценты за год. В Excel формула для расчета суммы через год = S*r+S. В результате получим:
Число исходов = 2n, где 2 – число исходов (банкрот, не банкрот), n – число банков. Т.к. банка 3, то 23=8 исходов. Построим таблицу для всех возможных исходов, посчитаем их вероятность и общую сумму вкладов:
p – вероятность разорения, q=1-p – вероятность, что банк не разорится. Pобщ – равно произведению соответствующих значений в столбцах PА, PБ, PГ( т.к. события обанкротился банк или нет – независимые). Sобщ. рассчитывается по формуле: = СУММПРОИЗВ(SA1:SГ1;A(1):Г(1)). Для неё нужно построить ряд распределения(СВ S=(cyммa на всех счетах) и соответствующую гистограмму:
Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: Для вычисления мат. ожидания в Excel, используется формула =СУММПРОИЗВ(Sобщ;pобщ), где: Sобщ. - сумма полученная вкладчиком (Х); pобщ – вероятность данного события (Р(х)). В результате вычислений мат. ожидание равно: M(x) = 2,32. Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: Для вычисления дисперсии в Excel составляется следующая формула =СУММПРОИЗВ(Sобщ;pобщ;Sобщ)-М(x)*М(х). В результате дисперсия равна: D(x) = 0,531424. Среднее квадратичное отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: Для вычисления σx в Excel из значения дисперсии был извлечен квадратный корень =КОРЕНЬ(D(x)).Среднее квадратичное отклонение равно: σx =0,728988. Среднее абсолютное отклонение высчитывается по формуле В Excel САО высчитывается по формуле: =СУММПРОИЗВ(ABS(Sобщ-М(х));pобщ), В результате вычислений САО =0,1845.
|



 3). По полученным данным строим гистограмму:
3). По полученным данным строим гистограмму: . Её значения находим суммированием вероятностей. В результате
. Её значения находим суммированием вероятностей. В результате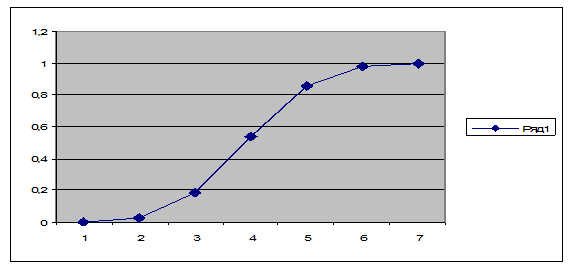
 . Для вычисления мат. ожидания в Excel, используется функция СУММПРОИЗВ(Х;Рх). В результате вычислений мат. ожидание равно:
. Для вычисления мат. ожидания в Excel, используется функция СУММПРОИЗВ(Х;Рх). В результате вычислений мат. ожидание равно: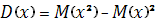




 D
D



 1 4 4
1 4 4
 5 C ≡ A 6 → 6 = 5 C ≡
5 C ≡ A 6 → 6 = 5 C ≡
 A 3 A 2 3
A 3 A 2 3

 D D D D
D D D D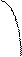

 4 4
4 4
 ≡ 7 → 7 = 5 C ≡ 5 8 → 8 = C
≡ 7 → 7 = 5 C ≡ 5 8 → 8 = C A 3 3
A 3 3
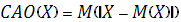 .
.


