Введение. Проблема численного решения систем линейных уравнений интересует математиков уже несколько столетий
Проблема численного решения систем линейных уравнений интересует математиков уже несколько столетий. Первые результаты появились в XVIII веке. В 1750 году Г. Крамер (1704-1752) опубликовал способ решения систем линейных алгебраических уравнений, в которых число неизвестных равно числу уравнений, с ненулевым определителем основной матрицы. Этот способ известен как правило Крамера. Гаусс в 1809 году опубликовал работу, посвященную движению небесных тел, в которой был изложен метод для решения линейных систем, известный как метод исключения. В 40-х годах XX века с появлением компьютеров сильно возрос интерес к численным методам. Тогда же началось активное исследование существующих методов для их реализации на ЭВМ и предпринимались активные попытки увеличить их точность. Вплоть до 80-х годов решение вычислительных задач было ограничено ресурсами ЭВМ, поэтому особое значение придавалось экономичности алгоритмов. В настоящее время ограничения по оперативной памяти и быстродействию ЭВМ потеряли актуальность в связи с появлением относительно дешевых мини- и суперкомпьютеров, но только при небольшом числе переменных систему линейных уравнений можно решать любым способом. Если же число переменных большое, то при неудачном выборе метода решения линейной системы уравнений время, затраченное компьютером на вычисления, может быть слишком большим. Для решения системы из n уравнений с n неизвестными приходится выполнять порядка n3 операций. Кроме того, при большом числе операций могут сильно возрастать погрешности, связанные с округлениями в компьютере результата каждой операции. Для решения системы n линейных уравнений с n неизвестными и невырожденной матрицей коэффициентов используется разложение матрицы коэффициентов в произведение более простых матриц. Пусть дана система линейных уравнений
где
– соответственно матрица коэффициентов, столбец неизвестных и столбец свободных членов соответственно. Пусть матрица
Обозначим
|

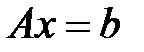 , (1)
, (1)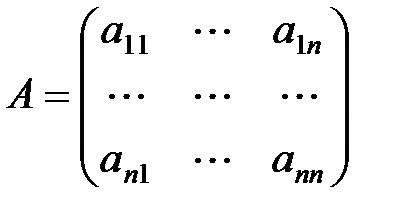 ,
, 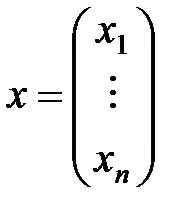 ,
, 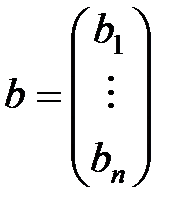
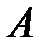 невырожденная, т.е.
невырожденная, т.е. 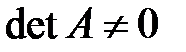 . Пусть
. Пусть  , где
, где 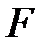 и
и  – квадратные матрицы порядка n, такие, что системы
– квадратные матрицы порядка n, такие, что системы  ,
, 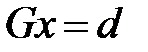 легко решаются. Тогда система (1) принимает вид
легко решаются. Тогда система (1) принимает вид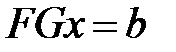 . (2)
. (2)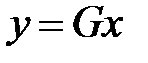 . Система (2) запишется в виде
. Система (2) запишется в виде  , и ее решение легко найти. Пусть ее решение уже найдено. Тогда из системы
, и ее решение легко найти. Пусть ее решение уже найдено. Тогда из системы 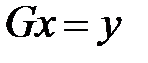 находим x. Эта система тоже легко решается. Мы рассмотрим только три способа разложения матриц, разложения LU, QR и Холецкого. Задумываться о выборе определенного метода имеет смысл в том случае, если необходимо найти решение системы линейных уравнений с большим числом неизвестных. Для систем с маленьким числом неизвестных выбор метода зависит от вида матрицы (для метода Холецкого требуется симметричная матрица коэффициентов).
находим x. Эта система тоже легко решается. Мы рассмотрим только три способа разложения матриц, разложения LU, QR и Холецкого. Задумываться о выборе определенного метода имеет смысл в том случае, если необходимо найти решение системы линейных уравнений с большим числом неизвестных. Для систем с маленьким числом неизвестных выбор метода зависит от вида матрицы (для метода Холецкого требуется симметричная матрица коэффициентов).


