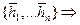Понятие диагонализируемости линейного оператора
Определение: Линейный оператор j в R n, называется диагонализируемым, если в некотором базисе f его матрица имеет вид:
Теорема: (критерий диагонализируемости оператора) Линейный оператор j в R n диагонализируем тогда и только тогда, когда существует базис в R n состоящий целиком из собственных векторов j. Доказательство: Пусть оператор j - диагонализирован
Þfi – собственный вектор, отвечающий собственным значениям ci. Доказательство: (в обратную сторону) Пусть
Теорема: (достаточные условия диагонализируемости оператора) Если число различных собственных значений линейного оператора равно n, то оператор диагонализируем: Доказательство:
|
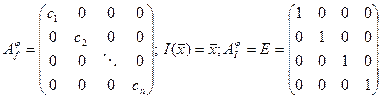
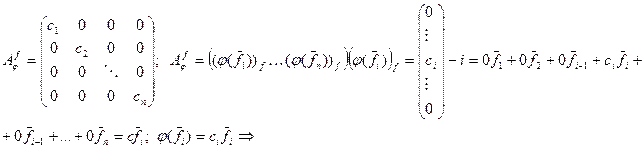
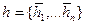- базис в R n, 
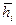- собственный вектор j, отвечающий собственным значениям li: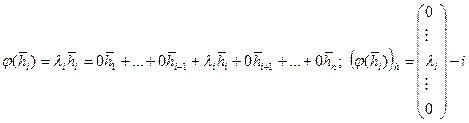
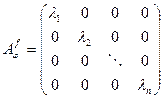Собственные вектора образуют линейное подпространство размерности 1 в базисе в R n из собственных векторов, нет.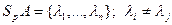
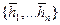- линейно независимы, так как в в R n n – максимальное число линейно независимых векторов Þ " 
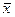Î R n линейных векторов через 
