Прямых измерений
Измерения одной и той же величины дают в общем случае результаты, несколько отличающиеся друг от друга даже тогда, когда они производились одним и тем же лицом, одним и тем же способом, посредством одних и тех же приборов. Допустим, что мы произвели n прямых (непосредственных) измерений некоторой физической величины, истинное значение которой (нам неизвестное) обозначим через x. Обозначим через x1, x2, x3, …, xn результаты отдельных измерений, а через D xi = x - xi – абсолютную погрешность n -го измерения. Абсолютной погрешностью измеряемой величины называется разница между истинным и измеренным значениями этой величины. Абсолютная погрешность измеряется в единицах измеряемой величины. Тогда результаты измерений можно представить в виде: xi = x - D xi, где i =1, 2, 3, …, n (2.1) Естественно, что абсолютные погрешности D xi могут принимать как положительные, так и отрицательные значения. Суммируя левую и почленно правую стороны равенств (2.1), имеем:
Разделив обе стороны равенства (2.2) на число измерений п, получим после перестановки членов:
где Если число измерений п достаточно велико (строго говоря, при n ®¥), получим равенство:
так как в серии из большого числа измерений всякой положительной погрешности можно сопоставить равную ей по абсолютной величине отрицательную погрешность. Из (2.3) и (2.5) следует: при т.е. при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению. Однако при ограниченном числе измерений n среднеарифметическое значение будет отличаться от истинного значения, т.е. равенство (2.6) будет не точным, а приближенным: Нам необходимо оценить величину этого расхождения. Появление того или иного значения xi, в процессе измерения является случайным событием. Существует некоторая вероятность появления этого значения в интервале ( Задавая вероятность того, что истинное значение измеряемой величины x попадает в данный доверительный интервал, другими словами, задавая надежность α по числу проведенных измерений n можно определить значение коэффициента Стьюдента ta,n (см. приложение 7) и, следовательно, найти случайную абсолютную погрешность Δ x случ:
Эта погрешность является только частью совершаемой ошибки, обусловленной случайными причинами. Полная же абсолютная погрешность складывается из случайной погрешности и погрешности измерительного прибора. Последняя при выполнении лабораторных работ физического практикума, если неизвестен класс точности прибора, может быть определена как наименьшая цена деления измерительного прибора
Тогда полная абсолютная погрешность измеряемой величины может быть рассчитана так:
Далее под После того, как полная абсолютная погрешность посчитана, результат измерений можно записать в виде:. Это означает, что истинное значение величины x с надежностью α попадает в этот доверительный интервал. Следует отметить, что величина абсолютной погрешности Δ x результата измерений сама по себе еще не определяет точности измерений. Пусть, например, измеряя длину карандаша рулеткой, разделенной на сантиметры, мы получили, что эта длина равна l =18,0±0,5 см(±0,5 см составляет погрешность ленты рулетки). Если при помощи этой же рулетки мы измерим диаметр карандаша, то получим d =0,5±0,5 см. Хотя абсолютная погрешность измерений одинакова, точность измерений различна. Если в первом случае измерения достаточно точны, то во втором случае значение погрешности сравнимо по порядку с измеряемой величиной, что позволяют судить лишь о порядке величины. Для оценки точности измерений вводится понятие относительной погрешности ε, равной отношению абсолютной погрешности Δ x результата измерений к среднему значению:
В таком виде эта погрешность выражается в долях от единицы. Если же умножить ее на 100%, то она будет представлена в процентах:
За меру точности измерения принимают величину, обратную ε. Следовательно, чем меньше относительная погрешность e, тем выше точность измерений.
|

 . (2.2)
. (2.2)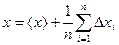 , (2.3)
, (2.3)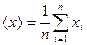 – среднеарифметическая величина. (2.4)
– среднеарифметическая величина. (2.4)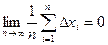 , (2.5)
, (2.5)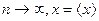 , (2.6)
, (2.6) .
. ), а следовательно, и появления соответствующего значения абсолютной погрешности D xi.
), а следовательно, и появления соответствующего значения абсолютной погрешности D xi. . (2.7)
. (2.7) :
: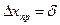 . (2.8)
. (2.8)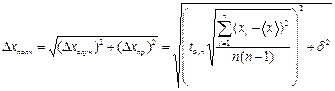 . (2.9)
. (2.9) будем понимать полную абсолютную погрешность измеряемой величины.
будем понимать полную абсолютную погрешность измеряемой величины.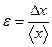 . (2.10)
. (2.10) . (2.11)
. (2.11)


