Случайных величин
Получение в серии измерений, проводимых в одинаковых условиях, несколько отличающихся значений одной и той же величины говорит о влиянии случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат измерения многих случайных возмущений и сама является случайной величиной. В этом случае можно лишь с определенной долей уверенности утверждать, что истинное значение случайной величины находится в пределах разброса результатов измерений: от минимального до максимального. Но неясно, какое из множества находящихся в этом промежутке значений принять за результат измерения и какова его случайная погрешность. Существует подход рассмотрения результатов измерений и случайных погрешностей как случайных величин. Количественные оценки в этом случае позволяют сделать методы теории вероятностей и математической статистики. Английский математик Скарборо предложил модель «случайностей» для экспериментального получения распределения случайных погрешностей. Нужно взять лист бумаги, разграфить его на
Смысл функции плотности распределения вероятностей случайной величины
В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным (Гауссовым) и равномерным распределением плотности вероятностей. Нормальное распределение случайных погрешностей возникает тогда, когда на результат измерений действует множество случайных возмущений, ни одно из которых не является преобладающим. На практике суммарное воздействие даже небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному. В аналитической форме нормальный закон распределения случайных величин в 1821 г. предложил немецкий математик Карл Гаусс:
где, xi – случайная величина; < x > – среднее арифметическое; σ; – среднее квадратическое отклонение. Перенеся начало координат в центр распределения < x > и откладывая по оси абсцисс погрешность Δ x = x - < x >, получим кривую нормального распределения погрешностей (рис. 6):
Для результатов n измерений, распределенных по нормальному закону:
Можно отметить следующие основные свойства нормального распределения. 1. Кривая нормального распределения f (Δx) (рис. 6) имеет колоколообразную форму. Характеристиками кривой являются: а) среднее значение
3. Малые погрешности встречаются чаще, чем большие. 4. Кривая нормального распределения погрешностей относительно вертикальной оси, проходящей через наивысшую точку кривой, симметрична, т.е. одинаковые погрешности, но с различными знаками имеют одинаковую вероятность.
Сравнивая кривые между собой можно видеть, что чем меньше среднее квадратичное отклонение, тем меньше рассеяние результатов измерений и тем больше вероятность того, что большинство случайных погрешностей в них будет мало. Естественно заключить, что качество измерений тем выше, чем меньше среднее квадратичное отклонение случайных погрешностей.
Δ х (α) = t×σ;, (1.6) где t – коэффициент, зависящий от α и формы закона распределения. На графике нормального распределения погрешностей (рис. 8) по оси абсцисс отложены интервалы с границами ± σ;, ±2 σ;, ±3 σ;, ±4 σ;. Доверительные вероятности для этих интервалов приведены в таблице 1. Как видно из этой таблицы, оценка случайной погрешности группы измерений интервалом ±1 σ; соответствует доверительной вероятности 0,68. Такая оценка не дает уверенности в высоком качестве измерений, поскольку 32% от Для единообразия в оценке случайных погрешностей при технических измерениях доверительную вероятность α принимают равной 0,95. Лишь для особо точных и ответственных измерений (важных, например, для безопасности и здоровья людей) применяют более высокую доверительную вероятность.
|

 ряд полос шириной 1 см, через середину средней полосы провести цветную линию, которая будет служить прицельной линией. Затем взять карандаш за неоточеный конец двумя пальцами и, прицеливаясь в среднюю линию, отпустить его с высоты одного метра. Карандаш, ударяясь о бумагу, оставит след – точку (рис. 3). Бросая карандаш 50–100 раз, получим совокупность точек, расположенных на различных полосках листа. Полученные результаты можно представить наглядно, построив диаграмму, которая показывала бы, как часто получались при измерениях те или иные значения. Для этого весь диапазон измеренных значений, отложенных по горизонтальной оси, разбивают на равные интервалы, ширина которых Δ x может быть любой и выбирается так, как это удобно. Затем подсчитывают число m значений измеренной величины, попавших в каждый интервал, и на каждом интервале строят прямоугольник с основанием, равным ширине интервала, и высотой, равной числу значений измеренной величины, попавших в данный интервал (в соответствии с выбранной масштабной единицей). В результате получается диаграмма, изображенная на рис. 4. Такая диаграмма называется гистограммой.
ряд полос шириной 1 см, через середину средней полосы провести цветную линию, которая будет служить прицельной линией. Затем взять карандаш за неоточеный конец двумя пальцами и, прицеливаясь в среднюю линию, отпустить его с высоты одного метра. Карандаш, ударяясь о бумагу, оставит след – точку (рис. 3). Бросая карандаш 50–100 раз, получим совокупность точек, расположенных на различных полосках листа. Полученные результаты можно представить наглядно, построив диаграмму, которая показывала бы, как часто получались при измерениях те или иные значения. Для этого весь диапазон измеренных значений, отложенных по горизонтальной оси, разбивают на равные интервалы, ширина которых Δ x может быть любой и выбирается так, как это удобно. Затем подсчитывают число m значений измеренной величины, попавших в каждый интервал, и на каждом интервале строят прямоугольник с основанием, равным ширине интервала, и высотой, равной числу значений измеренной величины, попавших в данный интервал (в соответствии с выбранной масштабной единицей). В результате получается диаграмма, изображенная на рис. 4. Такая диаграмма называется гистограммой. Если количество измерений увеличивать
Если количество измерений увеличивать 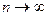 , а величину интервала уменьшать (интервалы не могут равняться нулю, но могут быть бесконечно малыми (dx) и приняты за точку), то гистограмма стремится перейти в плавную кривую, линию, приближающуюся к кривой, называемой кривой плотности распределения вероятностей случайной величины или кривой Гаусса (рис. 4), а уравнение, описывающее ее, – дифференциальным законом распределения.
, а величину интервала уменьшать (интервалы не могут равняться нулю, но могут быть бесконечно малыми (dx) и приняты за точку), то гистограмма стремится перейти в плавную кривую, линию, приближающуюся к кривой, называемой кривой плотности распределения вероятностей случайной величины или кривой Гаусса (рис. 4), а уравнение, описывающее ее, – дифференциальным законом распределения.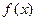 состоит в том, что
состоит в том, что 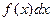 показывает долю значений величины, приходящихся на интервал
показывает долю значений величины, приходящихся на интервал 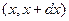 (рис. 5). На языке теории вероятностей
(рис. 5). На языке теории вероятностей 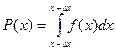 (1.1)
(1.1) дает вероятность того, что отдельное значение х окажется в интервале
дает вероятность того, что отдельное значение х окажется в интервале 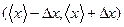 . Как правило указанный интеграл нормируют на единицу, т.е. всю площадь под кривой
. Как правило указанный интеграл нормируют на единицу, т.е. всю площадь под кривой  в интервал
в интервал 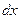 . На рис. 5 площадь, равная
. На рис. 5 площадь, равная 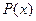 , указана редкой штриховкой,
, указана редкой штриховкой, 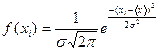 , (1.2)
, (1.2)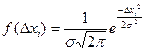 . (1.3)
. (1.3)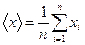 , (1.4)
, (1.4)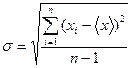 . (1.5)
. (1.5) , которое при очень большом числе измерений (
, которое при очень большом числе измерений ( , называемое среним квадратичным отклонением или средней квадратической погрешностью отдельного измерения.
, называемое среним квадратичным отклонением или средней квадратической погрешностью отдельного измерения.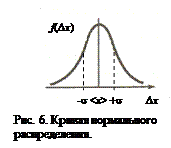 2. Вершина кривой соответствует наибольшему числу повторений, т.е. наиболее вероятному значению.
2. Вершина кривой соответствует наибольшему числу повторений, т.е. наиболее вероятному значению.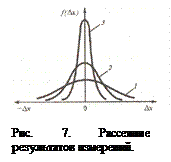 На рис. 7 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ1 > σ2 > σ3.
На рис. 7 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ1 > σ2 > σ3.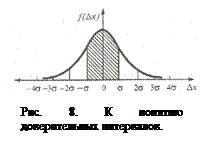 Интервал с границами ±Δ х называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность α – доверительной вероятностью. Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. Доверительные границы случайной погрешности Δ х (α), соответствующие доверительной вероятности α, находят по формуле:
Интервал с границами ±Δ х называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность α – доверительной вероятностью. Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. Доверительные границы случайной погрешности Δ х (α), соответствующие доверительной вероятности α, находят по формуле: всего числа наблюдений может выйти за пределы указанного интервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3 σ; соответствует α=0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3 σ; предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.
всего числа наблюдений может выйти за пределы указанного интервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3 σ; соответствует α=0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3 σ; предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.


