Оценка абсолютной погрешности прямых измерений
Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность. Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок. Все остальные погрешности являются случайными.
Промахи - грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами: 1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия. Абсолютная погрешность через класс точности оценивается следующим образом: (Dx) к.т.= (g/100)A, где g - класс точности в %, указанный на панели прибора, А = Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора: (Dx) ц.д.=
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения. Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда, который предписывает следующий образ действий, если физическая величина х измерена n раз: 1) имея х1, …,хn – значений измеряемой величины х, выбираем из 2) находим абсолютную погрешность Dxр = 3) Записываем результат в виде: Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.) Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1,...,m значений случайной величины 2) По оставшимся n значениям определяем среднее значение величины
3) Определяем среднеквадратичную погрешность среднего значения
4) Задаемся доверительной вероятностью a. По таблице коэффициентов Стьюдента определяем по известному значению числа измерений n и доверительной вероятности a коэффициент Стьюдента tan. 5) Определяем погрешность среднего значения величины D 6) Записываем результат
В научных статьях обычно приводят доверительный интервал Dх = s<X>, соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора. Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым. В теории ошибок показывается, что результирующая погрешность
|

 h,
h, хmax и хmin и находим среднее значение х:
хmax и хmin и находим среднее значение х: 
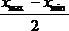
 с
с 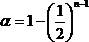 , где a - доверительная вероятность того, что истинное значение измеренной величины находится на отрезке
, где a - доверительная вероятность того, что истинное значение измеренной величины находится на отрезке 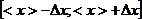
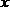 i. Сначала исключаем промахи, то есть заведомо неверные результаты.
i. Сначала исключаем промахи, то есть заведомо неверные результаты.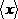 :
: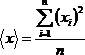 і
і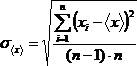 i
i = (
= (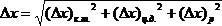 , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее – погрешность) эксперимента.
, если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее – погрешность) эксперимента.


