Способы борьбы с арифметическими ошибками.
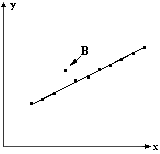
1. Избегайте ненужных выкладок. Чем меньше вы делаете выкладок, тем меньше вероятность ошибиться и тем больше умственной энергии вы сохраните для вычислений, которые действительно необходимы. 2. Пример: Допустим, что вы исследуете зависимость средней арифметической скорости молекул от температуры, Стоит ли рассчитывать шесть значений скоростей, каждый раз вычисляя выражение под корнем? Гораздо выгоднее рассчитать один раз выражение 3. Будьте аккуратны. Вычисления следует производить как можно последовательно и аккуратно. При этом записывайте их так, чтобы было много свободного места. Неаккуратная и неразборчивая запись выкладок часто оказывается причиной арифметических ошибок. Почти все, что было сказано о записи измерений, относится и к записи вычислений. 4. Проверка арифметических выкладок. Проверку следует рассматривать как необходимую часть вычислений. Вычисления можно разбить на две категории – «самопроверяющиеся» и «несамопроверяющиеся». Допустим, например, что мы измеряем две величины и после каких-то арифметических действий получаем пары числовых значений xi, yi. Результаты измерений наносим на график, и они укладываются приблизительно на прямую линию. В этом случае можно обойтись без очень тщательной проверки выкладок для каждой пары значений ибо на графике допущенная ошибка легко обнаруживается (рис.17).
Это пример самопроверяющихся вычислений. При вычислении координат точки B почти наверняка была допущена ошибка. Но предположим, что в конце опыта на основании полученных нами данных необходимо вычислить величину
В этом случае мы имеем дело с несамопроверающимися вычислениями. Если вы работаете с напарником, то лучше каждому из вас произвести расчет самостоятельно. Если оба результата согласуются, то почти наверняка оба верны. Если вы работаете один, то надо постараться привести проверки выкладок другим способом. Некоторые могут подумать, что вычислять результат двумя способами – излишняя предосторожность. Но ошибки вычислений – главная причина того, что экспериментатору приходится понапрасну тратить время. Тщательная же проверка в итоге приводит к сбережению времени. Помните, что если в учебной лаборатории кто-то может проверить вашу работу и найти ошибки, то потом уже никто не сделает этого. Вы должны выработать у себя привычку при вычислениях всегда прикидывать результат в уме хотя бы с точностью 30% Например, в случае выражения (25) следует прикинуть в уме примерно так:
Значит, z ≈ 4000. Если при проверке получен результат, не согласующийся с первоначальным, то сначала пересмотрите ход проверочного расчета, ибо он наверняка проводился менее аккуратно. Рассказывают, что один новенький аспирант–теоретик как-то принес показать результаты сложных расчетов своему руководителю, известному физику. Проглядев их, руководитель сказал: «Если взять следующий частный случай, то ваш результат должен свестись к тому-то и тому». Он набросал на обложке две строчки выкладок и сказал: «Видите, не получается. Вы где-то ошиблись». Смущенный аспирант забрал работу и потратил целый месяц, чтобы повторить все заново. Потом снова пришел к руководителю. – Ну, как, – спросил именитый ученый, – нашли ошибку? – Да, – ответил тот, – в двух строчках ваших выкладок.
|

 и взяли лишь шесть значений температуры: T1, T2,..., T6.
и взяли лишь шесть значений температуры: T1, T2,..., T6.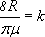 и затем найти шесть значений скоростей по формуле
и затем найти шесть значений скоростей по формуле 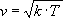 .
.
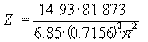 . (25)
. (25)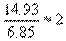 ;
;


