Обработка результатов прямого измерения
Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины: x1, x2, x3,... xn. (2) Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Величину, которая будет являться такой оценкой, мы обозначим µ = Так как оценочные значения результата измерений Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде l = (8.34 ± 0.02) мм, (P = 0.95) Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм. Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений Эта задача может быть решена с помощью теории вероятностей и математической статистики. В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой
где Δx – отклонение от величины истинного значения; σ – истинная среднеквадратичная ошибка; σ 2– дисперсия, величина которой характеризует разброс случайных величин.
Как видно из (4) функция имеет максимальное значение при x = 0, кроме того, она является четной. На рис.16 показан график этой функции. Смысл функции (4) заключается в том, что площадь фигуры, заключенной между кривой, осью Δx и двумя ординатами из точек Δx1 и Δx2 (заштрихованная площадь на рис.16) численно равна вероятности, с которой любой отсчет попадет в интервал (Δx1,Δx2). Поскольку кривая распределена симметрично относительно оси ординат, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны. А это дает возможность в качестве оценки результатов измерений взять среднее значение всех элементов выборки (2)
где – n число измерений. Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина Средней квадратичной ошибкой отдельного результата измерения называется величина
Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ σ = lim S. (7) С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений. Среднеквадратичной ошибкой среднего арифметического называется величина
Это фундаментальный закон возрастания точности при росте числа измерений. Ошибка
Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз. В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него. Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом Стьюдента t. Опуская теоретические обоснования его введения, заметим, что Δx = где Δx – абсолютная ошибка для данной доверительной вероятности; Коэффициенты Стьюдента приведены в таблице 2. Из сказанного следует: 1. Величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического. 2. При n → ∞ Для этого удобнее воспользоваться таблицей 3, в которой интервалы заданы в долях величины σ, являющейся мерой точности данного опыта по отношению к случайным ошибкам.
Таблица 2
Таблица 3
При обработке результатов прямых измерений предлагается следующий порядок операций: 1. Результат каждого измерения запишите в таблицу. 2. Вычислите среднее значение из n измерений
3. Найдите погрешность отдельного измерения
4. Вычислите квадраты погрешностей отдельных измерений (Δx 1)2, (Δx 2)2,..., (Δx n)2. 5. Определите среднеквадратичную ошибку среднего арифметического
6. Задайте значение надежности (обычно берут P = 0.95). 7. Определите коэффициент Стьюдента t для заданной надежности P и числа произведенных измерений n. 8. Найдите доверительный интервал (погрешность измерения) Δx = 9. Если величина погрешности результата измерения Δx окажется сравнимой с величиной погрешности прибора δ, то в качестве границы доверительного интервала возьмите
Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте. 10. Окончательный результат запишите в виде
11. Оцените относительную погрешность результата измерений
Рассмотрим на числовом примере применение приведенных выше формул.
Пример. Измерялся микрометром диаметр d стержня (систематическая ошибка измерения равна 0.005 мм). Результаты измерений заносим во вторую графу таблицы, находим Таблица 4
Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10). Δd = 0.01238 · 2.57 = 0.04 мм. Сравним случайную и систематическую ошибки:
следовательно, δ = 0.005 мм можно отбросить. Окончательный результат запишем в виде d = (4.01 ± 0.04) мм при Р = 0.95.
§ 4. Округление результатов Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» – считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.
Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов. Правила округления Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.
Примеры:
Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности. Примеры: 243.871 ± 0.026 ≈ 243.87 ± 0.03; Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5. Примеры: 8.337 (округлить до десятых) ≈ 8.3; Если первая из отбрасываемых цифр больше или равна 5, (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу. Примеры: 8.3351 (округлить дл сотых) ≈ 8.34; Если отбрасываемая цифра равна 5, а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная. Примеры: 0.875 (округлить до сотых) ≈ 0.88; Примечание. Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например, 0,00807 – в этом числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7; первые три нуля незначащие. 8.12 · 103 – в этом числе 3 значащих цифры. Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 – верны целые и десятые доли. Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10-3 и 2,34·105. Подобная запись упрощает вычисления, особенно в случае формул, удобных для логарифмирования. § 5. Обработка косвенных измерений В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин: N = ƒ (x, y, z,...) (13) Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е. ¯N = ƒ (¯x, ¯y, ¯z,...) (14) Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных. Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам
или
где Формулой (15) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (16) применять целесообразно, если функция имеет вид произведения или частного аргументов. Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:
или
где Δx, Δy, Δz,... – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов x, y, z,.... Следует иметь в виду, что доверительные интервалы Δx, Δy, Δz,... должны быть взяты при одинаковой доверительной вероятности P1 = P2 =... = Pn = P. В этом случае надежность для доверительного интервала ΔN будет тоже P. Формулой (17) удобно пользоваться в случае, если функция N = ƒ(x, y, z,...) имеет вид суммы или разности аргументов. Формулой (18) удобно пользоваться в случае, если функция N = ƒ(x, y, z,...) имеет вид произведения или частного аргументов. Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:
При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений. Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯N найти абсолютную погрешность. Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий. При обработке результатов косвенных измерений предлагается следующий порядок операций: Все величины, находимые прямыми измерениями, обработайте в соответствии с правилами обработки результатов прямых измерений. При этом для всех измеряемых величин задайте одно и то же значение надежности P. Оцените точность результата косвенных измерений по формулам (15) – (16), где производные вычислите при средних значениях величин. Если случайная и систематическая ошибки по величине близки друг к другу, то сложите их по правилу сложения ошибок. Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте. Результат измерения запишите в виде: N = ƒ (¯x, ¯y, ¯z,...) ± Δƒ. Определите относительную погрешность результата серии косвенных измерений Пример 1.Находится объем цилиндра по формуле
где d – диаметр цилиндра, h – высота цилиндра. Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты: d = (4.01 ± 0.03) мм, h = (8.65 ± 0.02) мм, при одинаковой надежности Р = 0.95. Среднее значение объема, согласно (14) равно
Воспользовавшись выражением (18) имеем: ln V = ln π + 2 lnd + lnh - ln4;
Так как измерения производились микрометром, цена деления которого 0.01 мм, систематические ошибки
Систематическая ошибка оказывается сравнимой со случайной, следовательно
Таким образом, результат измерения оказывается V = (109 ± 2) мм3 при P = 0.95
Пример 2. Найти абсолютную и относительную погрешности для следующей функциональной зависимости:
В этом случае удобнее сначала искать относительную погрешность. Тогда
= d[ln(m1 + m2 - m3)] - d(ln2) - d(ln m1) - d(ln m2) =
До сих пор подразумевается математический смысл дифференциала, и знаки слагаемых учитываются. Раскроем теперь выражение d(m1 + m2 - m3) = dm1 + dm2 - dm3 и разделим почленно на знаменатель. Затем объединим все члены, содержащие дифференциалы одной и той же переменной:
Используя формулу (18), получим
Абсолютную случайную погрешность найдем из выражения Δτ = ε ·¯¯τ Используя формулу (16) получаем
Абсолютную систематическую ошибку найдем из выражения δτ = ε τ¯ Приведем таблицу расчета погрешностей для простейших функций.
|

 . Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx. В таком случае мы можем записать результат измерений в виде
. Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx. В таком случае мы можем записать результат измерений в виде (4)
(4)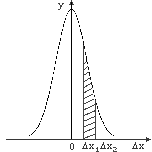
 , (5)
, (5)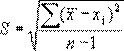 . (6)
. (6)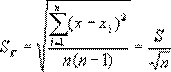 . (8)
. (8)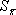 характеризует точность, с которой получено среднее значение измеренной величины
характеризует точность, с которой получено среднее значение измеренной величины 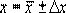 , (9)
, (9) .
.
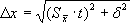 .
.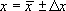 .
.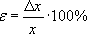 .
. , а в четвертую – их квадраты (таблица 4).
, а в четвертую – их квадраты (таблица 4).
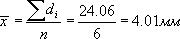

 ,
,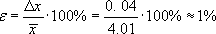
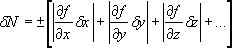 (15)
(15)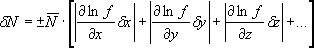 , (16)
, (16)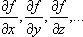 частные производные функции N = ƒ(x, y, z,...) по аргументу x, y, z..., найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные; δx, δy, δz – систематические ошибки аргументов.
частные производные функции N = ƒ(x, y, z,...) по аргументу x, y, z..., найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные; δx, δy, δz – систематические ошибки аргументов. (17)
(17)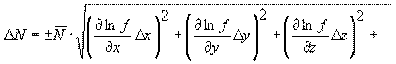 , (18)
, (18) .
. 

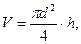

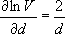 ;
;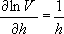 ;
;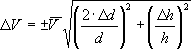 ;
; 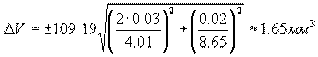 .
.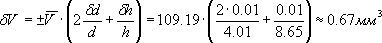 .
.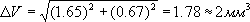 .
. .
. .
.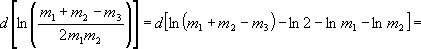
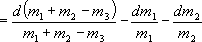 .
.
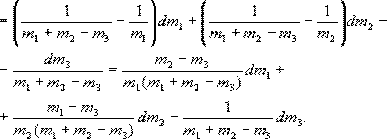 .
. .
. .
.


