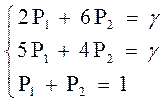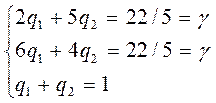ТЕМА 6 – ТЕОРИЯ ИГР
1. Основные понятия теории игр 2. Решение матричных игр, имеющих седловую точку 3. Решение матричных игр без седловой точки 4. Упрощение игр
В-1 Финансовые операции в условиях рыночных отношений часто характеризуется наличием противоположных интересов сторон. Они пытаются достичь своих целей часто в ущерб друг другу. Ситуации, в которых эффективность принимаемых одной из сторон решений зависит от другой стороны, называются КОНФЛИКТНЫМИ. Теория, занимающаяся принятием решений в конфликтной ситуации, называется ТЕОРИЕЙ ИГР, а математическая модель конфликтной ситуации – ИГРОЙ.
В отличие задач принятие решений в условиях определенности и неопределенности, в которых природа предполагалась пассивной, в теории игр имеются противодействующие стороны, интересы которых противоположны. Игра имеет место, если: 1. имеется несколько конфликтующих сторон (игроков); 2. каждый из них принимает решение по заданному набору правил; 3. каждому лицу известно возможное конечное состояние конфликтной ситуации; 4. Для каждой из сторон заранее определены платежи (выигрыши, проигрыши)
ЗАДАЧА ТЕОРИИ ИГР – выбрать такую линию поведения данного игрока, отклонения от которой может лишь уменьшить его выигрыш, т. е. рациональные действия. В настоящее время существуют: 1. Антагонистические игры (увеличение выигрыша одной из сторон на определенную величину ведет к уменьшению выигрыша другой стороны и наоборот) 2. Неантагонистические (кооперативные) игры 3. конечные 4. бесконечные игры 5. позиционные игры 6. дифференциальные игры 7. рефлексивные игры
Ситуация называется КОНФЛИКТНОЙ, если в них участвуют стороны, интересы которой полностью или частично противоположны. ИГРА – это действительный или формальный конфликт, в котором имеются не менее 2-х участников, каждый из которых стремится к достижению собственных целей. Допустимые действия каждого из игроков, направленные на достижение цели называют ПРАВИЛАМИ ИГРЫ. Количественная оценка результатов игры – ПЛАТЕЖ.
Игра называется ПАРНОЙ, если в ней участвуют 2 стороны, и МНОЖЕСТВЕННОЙ, если – более 2-х сторон. Участники игры могут образовывать коалиции (коалиционные игры). Множественная игра превращается в парную, если в ней участники образуют 2 постоянные коалиции. ИГРА С НУЛЕВОЙ СУММОЙ – это парная игра, в которой проигрыш одного игрока равен выигрышу другого, т. е. сумма платежей равна нулю. Игра называется КОНЕЧНОЙ, если число стратегий игроков конечно, иначе – бесконечно. Однозначное описание выбора игрока каждой из возможных ситуаций, когда он должен сделать личный ход называется СТРАТЕГИЕЙ ИГРОКА.
Стратегия называется ОПТИМАЛЬНОЙ, если она обеспечивает игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от поведения противника. Выбор одной из предусмотренных правилами игры стратегий ее осуществления называется ХОДОМ. Он бывает личным, если игрок сознательно выбирает и осуществляет вариант действий, и случайным, если выбор производится не игроком, а механизмом случайного действия.
Существует два способа описания игры: 1. ПОЗИЦИОННЫЙ, в виде развернутой формы, которая сводится к графу последовательных шагов (дерево игры). 2. НОРМАЛЬНЫЙ, в явном представлении совокупности стратегии игроков платежной функции. Парную игру с нулевой суммой обычно представляют в виде платежной матрицы (матричная игра).
Таблица – Платежная матрица
В парной игре с нулевой суммой выигрыш каждого игрока задается своей платежной матрицей, поэтому такие игры называются БИМАТРИЧНЫМИ. В платежной матрице строки соответствуют стратегиям первого игрока (всего их m), а столбцы – стратегии второго игрока (n). Данные стратегии называют чистыми. В результате первый игрок выигрывает величину αij, а второй – проигрывает. Первый игрок стремится максимизировать свой выигрыш, второй игрок – минимизировать свой проигрыш. Платежную матрицу называют конечной игрой размерностью m×n.
В-2 Решение матричных игр, имеющих седловую точку
Противники, участвующие в игре разумны, каждый из них делает все, чтобы добиться своей цели, исходя из этого наилучшая стратегия первого игрока, определяется следующим образом: Выбирая i-ую стратегию первый игрок должен рассчитывать, что второй игрок ответит на нее той из своих j-ых стратегий, при которой выигрыш первого игрока будет минимален. Найдем минимальное число в каждой строке матрицы, обозначим его λ и поместим в добавочный столбец (таблица - платежная матрица).
(1)
(2)
λ – гарантированный выигрыш первого игрока не меньший при любом поведении второго игрока, т. е. если это значение найти, то ВСЕГДА будет гарантированный выигрыш. λ – это нижняя цена игры, а стратегия первого игрока называется максиминной (перестраховочной). Второй игрок заинтересован уменьшить проигрыш, поэтому для выбора своей наилучшей стратегии он должен найти максимальное значение выигрыша первого игрокав каждом из столбцов ßj и среди данных значений выбрать наименьшее. (последняя строка в платежной матрице).
(3)
ß – верхняя цена игры, а стратегия второго игрока называется минимаксной. В любом случае он проиграет не более ß. Для нижней и верхней цен игры справедливо неравенство: λ < = ß (4) В играх, для которых нижняя цена равна верхней, т. е.
Оптимальные стратегии определяют положение равновесия в игре, т. е. каждый из игроков не заинтересован в отходе от этих стратегий, т. к. это не выгодно. Чистую цену игры в играх с седловой точкой при условии одинаковой разумности партнеров первый игрок не может увеличить, а второй – уменьшить, если игра имеет седловую точку, то она решается в чистых стратегиях, вероятность их применения равна 1.
Пример 1. Фирма может произвести 3 новых товара: А1, А2, А3. Она стремится продвинуть их на рынок, где возможна продажа конкурентами аналогичных товаров: В1, В2, В3. Фирме не известно, какой товар будет продавать конкурент, но известна вероятность продажи своих товаров при наличии на рынке новых конкурентов. Необходимо выбрать оптимальную стратегию для фирмы, т. е. товар, который будет иметь наилучшую вероятность продаж при любых действиях конкурента.
Решение:
1.Определим нижнюю цену игры
Min max 0,8 0,8 0,1 - 0 -
λ = max(0,8; 0,1; 0) = 0,8 (А1) 2.Определим верхнюю цену игры
Min(j) = 0,8
Для фирмы является оптимальной стратегия А1, т. е. выпуск товаров А1, для конкурента – тоже стратегия 1.
В – 3 Если игра, заданная матрицей не имеет Седловой точки, то поиск ее решения приводит к смешанной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными частотами. Вектор, каждый из компонентов которого показывает относительную частоту использования игроком соответствующей чистой стратегии называется СМЕШАННОЙ СТРАТЕГИЕЙ. Сумма компонентов вектора равна 1. Сами компоненты неотрицательны. Смешанные стратегии для первого игрока обозначим Р = (Р1, р2, …,Рm), Для второго игрока: Q = (q1, q2, …, qn).
Основная теорема теории игр:
Т. е. она лежит между нижней и верхней ценой.
Каждый игрок при многократном повторении игры, придерживаясь смешанной стратегии будет получать более выгодный результат. Стратегии игроков, входящих в оптимальные и смешанные стратегии называются АКТИВНЫМИ. Для решения игр: 2*2, 2*п, п*2, используется ТЕОРЕМА ОБ АКТИВНЫХ СТРАТЕГИЯХ: применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (минимальный средний проигрыш), равный цене игры гамма независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стретегий. Пример 2. Найти решение игры заданной матрицы:
Таблица
Предположим, что для первого игрока стратегия задается Р = (pi, p2,...,pm), тогда из теоремы 1 при применении первым игроком чистой стратегии 1 или 2 игрок первый получит средний выигрыш, равный цене игры, т.е.
Решив систему, получаем: Р1 = 2/5, Р2 = 3/5, гамма = 22/5. Найдем оптимальную стратегию для второго игрока: Q = (qi, q2... qn):
Из системы получаем, что ql = 1/5, q2 = 4/5
Т. о. решением игры является смешанная стратегия Р(2/5, 3/5) и Q(l/5, 4/5), а цена игры гамма = 22/5. В-4. В некоторых случаях задачу без седловой точки с большой размерностью можно упростить с помощью редуктирования, т.е. сведение игры со сложной матрицей к игре с более простой матрицей. Если в платежной матрице А(ау), где все элементы строки Ai(ai1, ai2,..., am) не меньше соответствующих элементов не которой строки Ak(akl, ak2,..., akn), а по крайней мере одна стока больше, то стока Ai называется доминирующей, а строка Ак - доминируемой. Аналогичны понятия «доминирующий» и «доминируемый» столбцы. Первому игроку не выгодно применять стратегии, которым соответствуют доминируемые стоки, а второму игроку - невыгодно применять стратегии которым соответствуют доминирующие столбцы. Следовательно, при решении игры можно уменьшить ее размерность путем удаления из платежной матрицы доминирующих столбцов и доминируемых строк.
Пример 3. Для игры с платежной матрицей
Найдите стратегии игроков и иену игры. Решение Элемент а32 = -1 является наименьшим в третьей строке и наибольшим во втором столбце, т. е. он является седловой точкой. Поэтому цена игры С = - 1, а оптимальные стратегии игроков: первого - А3, а второго – В2. Используя понятия доминируемых строк и доминирующих столбцов, задачу можно решить следующим образом. В матрице А третья строка доминирует над второй, поэтому вторую можно изъять из платежной матрицы. В результате получится матрица:
В матрице А1 первый и третий столбцы доминируют над вторым, следовательно, их можно изъять. В результате платежная матрица принимает вид:
В матрице А2, вторая строка доминирует. После вычеркивания получится матрица А3, состоящая из одного элемента:
А3 = (-1).
Элемент матрицы А3 и определяет решение нашей задачи. Отдельные игры могут не иметь седловых точек, т. е. у каждого игрока не существует единственной, наиболее надежной стратегии. В этом случае используют смешанную стратегию. Смешанная стратегия состоит в том, что в ходе игры происходит случайный выбор стратегии из некоторого множества смешанных стратегий и для каждой смешанной стратегии указывается вероятность ее выбора. Свойство оптимальности означает, что любое отступление одного из игроков от оптимальной стратегии (при условии, что второй игрок продолжает придерживаться своей оптимальной стратегии) при многократном повторении игры может только уменьшить его средний выигрыш (увеличить средний проигрыш). Решение игры обладает одним важным свойством: если игрок А использует свою оптимальную стратегию, а игрок В смешивает свои стратегии в любых пропорциях, то средний выигрыш игрока А не уменьшается. Стратегии, которые смешиваются для получения оптимальной стратегии, будем называть полезными. Доказано, что у игры т х п существует такое оптимальное решение, что число полезных стратегий с каждой стороны не превосходит минимального из чисел тип. Известно несколько методов нахождения оптимальных стратегий в играх двух лиц с нулевой суммой. Рассмотрим один из методов — метод линейного программирования для нахождения решения
|

 игроки
игроки
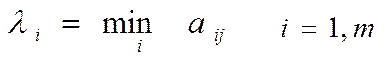

 Зная числа, игрок первый должен предпочесть ту стратегию, для которой - max
Зная числа, игрок первый должен предпочесть ту стратегию, для которой - max
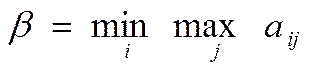
 λ = ß называется играми с седловой точкой. Общее значение нижней и верхней цены в играх с седловой точкой называют ЧИСТОЙ ЦЕНОЙ игры (). А стратегии, позволяющие достичь данного значения – оптимальными чистыми стратегиями. Оптимальные стратегии и чистая цена – это решение игры.
λ = ß называется играми с седловой точкой. Общее значение нижней и верхней цены в играх с седловой точкой называют ЧИСТОЙ ЦЕНОЙ игры (). А стратегии, позволяющие достичь данного значения – оптимальными чистыми стратегиями. Оптимальные стратегии и чистая цена – это решение игры. Игроки
Игроки







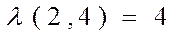 Нижняя цена игры:
Нижняя цена игры: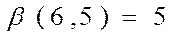 Верхняя цена игры:
Верхняя цена игры: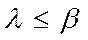 4 <= 5
4 <= 5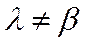 Т. к., то игра не имеет седловой точки, а ее решение является оптимальной смешанной стратегией. Цена игры принадлежит пределу от 4 до 5 включительно.
Т. к., то игра не имеет седловой точки, а ее решение является оптимальной смешанной стратегией. Цена игры принадлежит пределу от 4 до 5 включительно.