Погрешности косвенных измерений. Пусть измеряемая величина является функцией непосредственно измеряемых величин
Пусть измеряемая величина является функцией непосредственно измеряемых величин
Теория погрешностей определяет, что абсолютная погрешность ∆y находится по формуле
где ∂f/∂xi обозначает так называемую частную производную, т. е. производная, которая вычисляется от функции f по аргументу xi, причём все остальные аргументы считаются постоянными. Если измеряемые величины xi входят в основную формулу в виде произведения, то удобно определить вначале относительную погрешность по формуле
а затем найти и Рассмотрим применение формул (10) и (11) на примерах. Пусть
и по формуле (10)
причём ∆x1 и ∆x2 определены предварительно по формуле (4).
Пусть
В этом случае сначала найдём натуральный логарифм, а затем – частичные производные:
Подставляем в (11), найдём
Нетрудно видеть, что предварительное логарифмирование существенно упрощает вид частных производных. Возможен и другой подход к оценке погрешности результата косвенного измерения. Вместо определения искомой величины через среднее значение
Можно для каждого выполненного опыта вычислить
а затем найти Оба способа дают близкие результаты. Пусть, например, находится плотность цилиндрического тела: ρ = 4m / πD2H, причем непосредственно определяется три раза диаметр цилиндра Di и его высота Нi (i = 1, 2, 3). Тогда можно подсчитать ρi = 4m / πD2iHi. для каждого из трех измерений. Среднее значение плотности можно найти, как обычно, по формуле: <ρ> =∑ρi /3, а абсолютная погрешность определяется как Δρ = 4,3√[∑(<ρ> – ρi) /6]. Таблица 1.
|

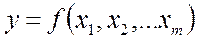 (9)
(9)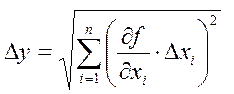 (10)
(10) (11)
(11)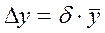
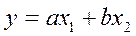 .
.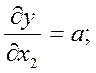
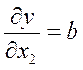
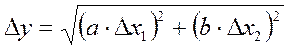 ,
,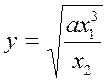 .
.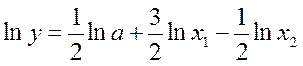
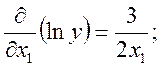
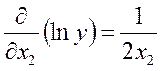


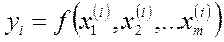
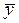 как среднее арифметическое и далее абсолютную погрешность по формуле (3).
как среднее арифметическое и далее абсолютную погрешность по формуле (3).


